CLASS-6
MEASUREMENT OF AN ANGLE
MEASUREMENT OF AN ANGLE -
The measurement of an angle refers to the amount of rotation required to bring one ray or line segment into coincidence with another, typically measured in degrees (°), radians, or other angular units. Here are the common units used for measuring angles:
- Degrees (°):- Degrees are the most common unit for measuring angles. A complete rotation around a point is divided into 360 degrees. Each degree is further divided into minutes (') and seconds ("). Example:- 45∘ means a 45-degree angle.
- Radians (rad):- Radians are another unit for measuring angles, particularly in trigonometry and calculus. One radian is the angle subtended when the radius of a circle sweeps an arc equal in length to the radius. The circumference of a circle is 2π radians. Example:- 4π radians is equivalent to a 45∘ angle.
- Gradians or Gon:- Gradians divide a right angle into 100 equal parts. A full circle in gradians is 400 gradians. Example:- 90∘ is equivalent to 100 gradians.
- Minutes ('') and Seconds ("):- Degrees can be further divided into minutes and seconds for more precise measurements. One degree is equal to 60 minutes, and one minute is equal to 60 seconds. Example:- 30∘ 15′ means 30 degrees and 15 minutes.
When measuring an angle, it's essential to consider the context and the unit of measurement being used. Be aware of the conventions and units relevant to the field of study or application. Understanding the measurement of angles is crucial in geometry, trigonometry, physics, engineering, and various other disciplines.
The size (magnitude & measure) of an angle is the amount by which one of the arm needs to be rotated about the vertex so that it lies on the top of the other arm.
In the adjoining figure, ∠1 is greater than ∠2.
In one hour, the minute hand of a clock makes one complete rotation. This is called one turn or one revolution.
Measurement of an Angle in Degree -
Most of the angles we deal are less than a complete turn, and hence their sizes are fractions of a turn. This is inconvenient to measure and it arises because a unit of one turn is very large. Therefore, we need a unit smaller than one turn for measuring angles. One turn is divided into 360 equal parts. Each part is called one degree and is usually written as 1∘ Thus -
1 turn (complete rotation) = 360∘
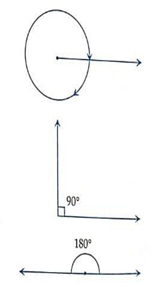
One turn is called a complete angle. A complete angle is equal to 360∘.
A quarter turn (1/4 turn) is called a right angle. A right angle is usually indicated by a square symbol near the vertex as shown in adjoining figure. A right angle is equal to 90∘.
A half turn (1/2 turn) is called a straight angle because the two arms of the angle make a straight line.
A straight line is equal to 180∘.
Example.1) What fraction of a clock wise revolution does the hour hand of a clock turn through when it comes from -
(i) 12 to 6, (ii) 6 to 9, (iii) 1 to 10.
Also find the number of right angles turned in each case.
Ans.)

(i) When the hour hand moves from 12 to 6 clockwise,
Fraction of revolution turned = 1/2
Number of right angles turned = 2 (Ans.)
(ii) When the hour hand moves from 6 to 9 clockwise,
Fraction of revolution turned = 1/4
Number of right angles turned = 1 (Ans.)
(iii) When the hour hand moves from 1 to 10 clockwise,
Fraction of revolution turned = 3/4
Number of right angles turned = 3 (Ans.)
Example.2) Which direction will you face if you start facing.
(i) east and make 1/2 of a revolution clockwise?
(ii) east and make 3/4 of a revolution anti clock wise?
(iii) west and make 3/4 of a revolution anti clock wise?
(iv) south and make one full revolution?
Should we specify clockwise or anti clockwise for part (iv)?
Ans.)
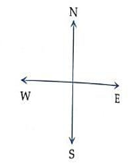
(i) West
(ii) South
(iii) North
(iv) South
No, in part (iv) it is immaterial whether we turn clockwise or anti-clockwise because one full revolution will bring us to the original position.