CLASS-6
INTERIOR & EXTERIOR ANGLE
INTERIOR & EXTERIOR ANGLE -
Interior and exterior angles are related concepts in geometry, often discussed in the context of polygons. These angles describe the angles formed within and outside of a polygon when its sides intersect. Let's explore them in more detail:
1. Interior Angles:-
- Interior angles are the angles formed inside a polygon when you draw diagonal lines from one vertex to another. In a polygon with n sides, there are n interior angles.
- The sum of the interior angles of a polygon can be calculated using the formula: (n−2) × 180∘, where n is the number of sides in the polygon. This formula holds for both regular and irregular polygons.
- Interior angles can vary in size depending on the shape of the polygon.
- In a convex polygon (a polygon where all interior angles are less than 180 degrees), the sum of the interior angles is always less than 180 degrees.
- Interior Angles are the angles formed within or inside a shape. Here, ∠ABC, ∠BCA and ∠CAB are interior angles.
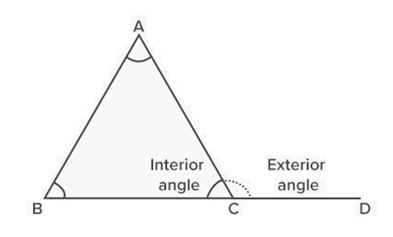
2. Exterior Angles:-
- Exterior angles are the angles formed outside a polygon at each vertex when one side of the polygon is extended. In a polygon with n sides, there are also n exterior angles.
- The exterior angle at each vertex is supplementary to the interior angle at the same vertex. This means that the exterior angle and the interior angle add up to 180 degrees.
- The sum of the exterior angles in any polygon, regardless of the number of sides, is always 360 degrees. This is because each exterior angle is supplementary to an interior angle.
- Exterior angles are the angles formed outside between any side of a shape, and a line extended from the adjoining side. Here, ∠ACD is an exterior angle.
Here's an example to illustrate the concept of interior and exterior angles:
Consider a pentagon (a polygon with five sides). The interior angles of the pentagon are the angles formed inside the polygon, and they can vary in size depending on the pentagon's shape. The exterior angles are the angles formed outside the pentagon at each vertex when you extend one side of the pentagon.
- The sum of the interior angles of a pentagon can be calculated using the formula: (5−2) × 180∘ = 3 × 180∘ = 540∘
- Each exterior angle at a vertex of the pentagon is supplementary to the interior angle at that vertex, so it measures 180∘ − interior angle.
Understanding interior and exterior angles is important in geometry, particularly when working with polygons, as they help determine the properties and relationships of the angles in these shapes.