CLASS-6
CONSTRUCTION OF PERPENDUCULAR BISECTOR OF A LINE SEGMENT
CONSTRUCTION OF PERPENDUCULAR BISECTOR OF A LINE SEGMENT -
Constructing the perpendicular bisector of a line segment involves a series of steps using a compass and a straightedge. Let's say you have a line segment AB, and you want to construct its perpendicular bisector:
- Draw the line segment:- Start by drawing the line segment AB using a ruler.
- Place the compass on one endpoint:- Put the compass needle on one endpoint of the line segment (point A, for example).
- Adjust the compass width:- Open the compass to a width greater than half the length of the line segment AB.
- Draw two arcs:- With the compass set at the adjusted width, draw arcs above and below the line segment. Make sure the arcs intersect the line. Label the points where the arcs intersect the line as C and D.
- Repeat with the other endpoint:- Move the compass to the other endpoint (point B) and draw similar arcs above and below the line segment, intersecting the line at points E and F.
- Connect the intersection points:- Use a straightedge to draw a line connecting the two intersection points on the line (C and D, or E and F). This line is the perpendicular bisector of the original line segment AB.
The reason this works is that the arcs drawn from each endpoint create points equidistant from the endpoints. Connecting these points forms a line that is perpendicular to the original line segment and passes through its midpoint, effectively bisecting it.
Remember, the steps may vary slightly depending on the specific instructions given or the tools available, but the general approach remains the same.
Another Way Of Understanding:-
To draw:- A perpendicular bisector of a line segment.
Given:- Any line segment AB.
Required:- To draw a perpendicular bisector of the line segment AB.
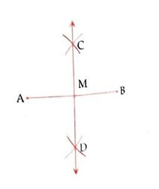
Steps Of Construction:-
Step.1) With A as centre and any suitable radius (>1/2 AB), draw arcs on each side of AB.
Step.2) With B as centre and same radius (as in step.1), draw arcs on each side of AB to cut the previous arcs at C & D.
Step.3) Draw a line passing through points C & D, then the line CD is the required perpendicular bisector of AB.