CLASS-6
CONSTRUCTION OF COPY OF AN ANGLE
CONSTRUCTION OF COPY OF AN ANGLE -
Constructing a copy of an angle involves creating an angle with the same measure as a given angle. Here's a step-by-step guide to constructing a copy of an angle using a compass and a straightedge:
Let's say you have angle ABC, and you want to construct an angle with the same measure.
Construction Steps:-
- Draw the Given Angle:- Use a ruler to draw the given angle, in this case, angle ABC.
- Place the Compass on Vertex A:- Open the compass wider than the width of the angle. Place the compass on the vertex A of the given angle.
- Draw an Arc:- Without changing the compass width, draw an arc that intersects both sides of the angle (AB and AC).
- Label the Intersection Points:- Label the intersection points of the arc with the sides of the angle as D and E.
- Place the Compass on Point D:- Without changing the compass width, place the compass on point D (the intersection point on one side of the angle).
- Draw Another Arc:- Draw an arc that intersects the first arc. Label the point of intersection as F.
- Draw a Line Through Points A and F:- Use a straightedge to draw a line through points A and F.
- Angle Copy:- The angle between AF and AD is a copy of the given angle ABC.
Note:- This construction works because the intercepted arcs AD and DE are congruent, and thus the angles at the center of the arcs (angles BAD and BAE) are congruent. As a result, the angle formed by lines AF and AD is a copy of angle ABC.
Always ensure that your constructions are precise, and use a sharp pencil and a good quality compass for accurate results.
Understanding by another way -
Let ∠AOB be angle whose measure is known and we want to make a copy of this angle. We want to construct an angle whose measure is equal to the measure of ∠AOB.
Steps Of Construction -
Step.1) Take any point 'P' and through 'P', draw ray PQ.
Step.2) With 'O' as centre and any (suitable) radius, draw an arc to meet ray OA at C and ray OB at D.
Step.3) Taking P as centre and same radius (as in step.2), draw an arc to meet PQ at R.
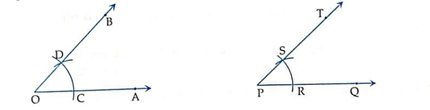
Step.4) Measure the segment CD with compass.
Step.5) With R as centre and radius equal to CD, draw an arc to meet the previous arc at S.
Step.6) Join PS and produce it to form a ray OT, then ∠QPT = ∠AOB.