CLASS-6
COMPLEMENTARY ANGLE
COMPLEMENTARY ANGLE -
Complementary angles are a pair of angles whose measures add up to 90∘. In other words, if you have two angles A and B such that A + B = 90∘, then A and B are complementary angles.
Mathematically, if A and B are complementary angles, we write:
A + B = 90∘
Here are a few key points about complementary angles:
- Sum of Measures:- The sum of the measures of complementary angles is always 90∘.
- Examples:-30∘ and 60∘ are complementary angles because 30∘ + 60∘ = 90∘. 45∘ and 45∘ are also complementary because 45∘ + 45∘ = 90∘.
- Right Angle:- Complementary angles are often associated with right angles. If one angle in a pair is a right angle (90∘), the other must be its complementary angle.
- Symbolically:- If A and B are complementary angles, we can express this relationship as A ⊥ B, where ⊥ represents perpendicularity.
- Complementary Angles in Trigonometry:- In trigonometry, complementary angles are frequently used. For example, in a right triangle, the two acute angles are complementary. If one angle is x∘, the other is (90∘−x∘).
- Complementary Pairs:- Complementary angles form pairs, and each angle in the pair complements the other.
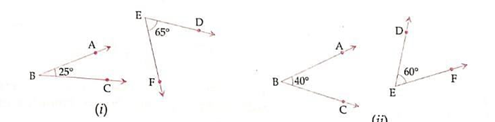
In fig (i),
∠ABC + ∠DEF = 25∘ + 65∘ = 90∘
So, sum of their measure is 90∘, therefore ∠ABC & ∠DEF are complementary.
In figure (ii),
∠ABC + ∠DEF = 40∘ + 60∘ = 100∘
So, sum of their measure is not 90∘, therefore ∠ABC & ∠DEF are not complementary.
Examples.1) Find the complement of 40 degrees.
Ans.)
As the given angle is 40 degrees, then, Complement is 50 degrees.
We know that Sum of Complementary angles = 90 degrees,
So 40° + 50° = 90° (Ans.)
Understanding complementary angles is important in various areas of mathematics, including geometry and trigonometry. They often arise in the study of right triangles and can be used to solve problems involving angles and their measures.