CLASS-6
ALGEBRA-DEGREE OF POLYNOMIAL
DEGREE OF POLYNOMIAL -
In algebra, the degree of a polynomial is a crucial characteristic that provides information about the polynomial's behavior and complexity. The degree of a polynomial is determined by the highest power (exponent) of the variable in any of its terms. Here are some key points about the degree of a polynomial:
- Degree Definition:- The degree of a polynomial is the highest exponent among all the terms in the polynomial.
- Variable's Exponent:- The exponent is associated with the variable(s) within each term. For example, in the term "2x³," the degree is 3 because it's the highest exponent of the variable "x."
- Constant Term:- If a polynomial contains only a constant term (no variable), its degree is considered to be 0 because there is no variable with an exponent greater than 0.
- Degree Notation:- The degree of a polynomial is often denoted by the variable "n." For example, if the degree of a polynomial is 4, it is referred to as a "quartic" polynomial.
Now, let's look at some examples to illustrate the concept of polynomial degrees:
- Linear Polynomial:- A linear polynomial has a degree of 1. For example, "3x + 2" is a linear polynomial, and its degree is 1 because the highest exponent of "x" is 1.
- Quadratic Polynomial:- A quadratic polynomial has a degree of 2. For example, "2x²- 5x + 1" is a quadratic polynomial, and its degree is 2 because the highest exponent of "x" is 2.
- Cubic Polynomial:- A cubic polynomial has a degree of 3. For example, "4x³- 2x²+ x - 7" is a cubic polynomial, and its degree is 3 because the highest exponent of "x" is 3.

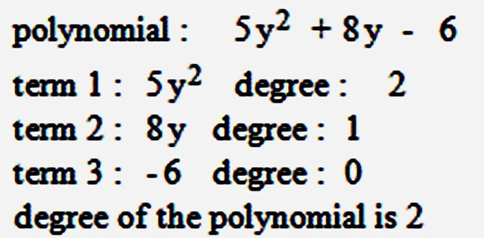
4. Constant Polynomial:- A constant polynomial (a constant term with no variable) has a degree of 0. For example, "7" is a constant polynomial, and its degree is 0.
5. Polynomial Function:- In a polynomial function, the degree is determined by the highest exponent of the variable in the function. For instance, the function "f(x) = 2x³- 5x²+ 4x - 7" is a cubic polynomial function because its highest exponent of "x" is 3, giving it a degree of 3.
Understanding the degree of a polynomial is important when analyzing its behavior, determining the number of roots or solutions, and classifying it based on its degree (linear, quadratic, cubic, etc.). The degree provides valuable insights into the polynomial's characteristics and properties.
When a polynomial has more than one variable, we need to look at each term. Terms are separated by + or - signs:
For each term:-
·Find the degree by adding the exponents of each variable in it, The largest such degree is the degree of the polynomial.
Example 1: What is the degree of this polynomial: 5xy²+3x-5y³+3
Checking each term:-
· 5xy²has a degree of 3 (x has an exponent of 1, y has 2, and 1+2=3)
· 3x has a degree of 1 (x has an exponent of 1)
· 5y³has a degree of 3 (y has an exponent of 3)
· 3 has a degree of 0 (no variable)
2yz has
a degree of 2 (y has an exponent of
1, z has 1, and 1+1=2)The largest
degree of those is 4, so the polynomial has a degree of 4
The largest degree of those is 3 (in fact two terms have a degree of 3), so the polynomial has a degree of 3.
Example 2: what is the degree of this polynomial 4z³+ 5y²z²+ 2yz Checking each term:
· 4z² has a degree of 3 (z has an exponent of 3)
· 5y²z² has a degree of 4 (y has an exponent of 2, z has 2, and 2+2=4)