CLASS-6
ALGEBRA - VARIABLE

CONCEPT OF VARIABLE -

In algebra, the concept of a variable is fundamental and plays a central role in solving equations, representing unknown quantities, and describing relationships between numbers and symbols. Here's a more detailed explanation of the concept of a variable in algebra:-

1. Symbolic Representation:- A variable is typically represented by a letter or symbol, often chosen from the end of the alphabet (such as x, y, z). These letters can represent any number, and their values are not fixed but can vary.

2. Unknown or Variable Quantity:- Variables are used to represent quantities that are not known or fixed. They stand for values that can change or are yet to be determined. For example, in the equation 2x + 3 = 7, the variable "x" represents an unknown number.

3. Equations:- Variables are commonly used in equations to express mathematical relationships. Equations typically involve one or more variables, along with constants and mathematical operations. Solving the equation involves finding the value(s) of the variable(s) that make the equation true. For example, in the equation x - 5 = 0, the variable "x" can be solved to find that x = 5.

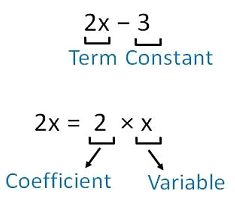
4. Expressions:- Variables are also used in algebraic expressions, which are combinations of variables, constants, and mathematical operations. These expressions can represent a wide range of mathematical relationships. For example, 2x - 3 is an algebraic expression involving the variable "x."

5. Functions:- In the context of functions, variables serve as input values. For example, in the function f(x) = 2x + 1, "x" is the variable representing the input value, and "f(x)" represents the corresponding output value.

6. Real-World Applications:- Variables are crucial for modeling and solving real-world problems. They allow us to represent changing quantities, such as time, distance, temperature, or financial values, with mathematical expressions. For instance, in physics, variables can represent the position of an object over time.

7. Graphing:- Variables are used to represent points on a graph. In the Cartesian coordinate system, "x" and "y" represent the horizontal and vertical positions of a point, respectively. Graphs help visualize relationships between variables.

8. Generalization:- Variables enable the generalization of mathematical ideas and patterns. They make it possible to express mathematical rules and formulas that apply to a wide range of situations.

In essence, variables in algebra are placeholders for numbers or values that can vary. They are used to represent unknowns, describe relationships between quantities, and solve mathematical and real-world problems. The ability to work with variables is a fundamental skill in algebra, enabling mathematicians and scientists to analyze, model, and solve a wide variety of mathematical and practical problems.