CLASS-6
ALGEBRAIC TERM
TERM -
An algebraic term is a basic component of an algebraic expression or equation. It is typically composed of a coefficient and one or more variables, possibly raised to certain powers. Algebraic terms can also include constants. Here are the key elements that make up an algebraic term:
- Coefficient:- The coefficient is a numerical factor that multiplies the variables or constants within the term. It represents the magnitude or scale of the term. Coefficients can be positive, negative, or zero.
- Variable(s):- Variables are symbols, often represented by letters, that stand for unknown or varying quantities. Variables are raised to specific powers, which may be integers or fractions.
- Exponent(s):- Exponents are the numerical values written as superscripts on variables. They indicate the power to which the variable is raised. For example, "x^2" has an exponent of 2, which means "x" is squared.
- Constant(s):- Constants are fixed numerical values that do not contain variables. They are standalone numbers that can be part of an algebraic term.
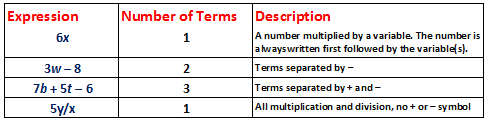
Algebraic terms are essential components of algebraic expressions and equations. They can be combined with other terms using mathematical operations such as addition, subtraction, multiplication, and division to create more complex algebraic expressions. Here are some examples of algebraic terms:
- Simple Term:- "2x" is a basic algebraic term. It has a coefficient of 2 and one variable "x" raised to the first power.
- Constant Term:- "5" is also an algebraic term, but it's a constant term because it doesn't contain any variables. The coefficient is 5, and there are no variables or exponents.
- Term with Exponent:- "3y^3" is an algebraic term with a coefficient of 3, the variable "y" raised to the third power, and no constants.
- Mixed Term:- "4xy^2" is a more complex algebraic term. It has a coefficient of 4, two variables "x" and "y," with "y" raised to the second power.
Algebraic terms can be combined to form algebraic expressions, which are composed of multiple terms connected by mathematical operations. These expressions can be simplified, manipulated, and used to represent various mathematical relationships and real-world situations in algebra.