CLASS-5
VOLUME AREA PERIMETER

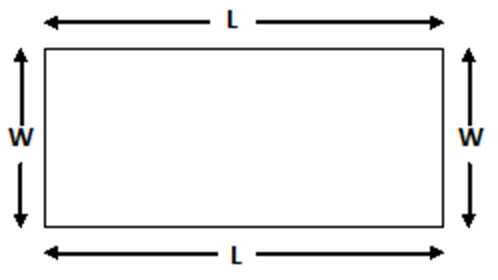
As we all know that, the above picture or diagram is of Rectangle and in Rectangle there are two opposite sides that are equal in the length and the width. Here ‘L’ defines length and ‘W’ defines width of this rectangle, therefore perimeter of a Rectangle is 

     =  L + W + L + W =  L + L + W + W  =  2 L + 2 W                                                                           

     = 2 ( L + W )  =  2 ( Length + Width)

The opposite side of Length and Width of Rectangle must be the same units while calculating the Perimeter of Rectangle

SQUARE  

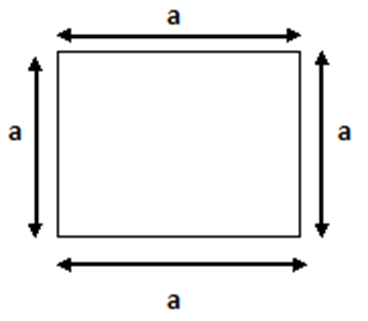
As we all know that, the above picture or diagram is of a Square and in a Square there are all sides should be equal in length. Here ‘a’ defines the length of each side of this rectangle, therefore perimeter of a Rectangle is 

=  a + a + a + a =  4 a

= 4 x Length of One side

Each opposite side of the Length and the Width of Rectangle must be the same units while calculating the Perimeter of Rectangle.

TRIANGLE

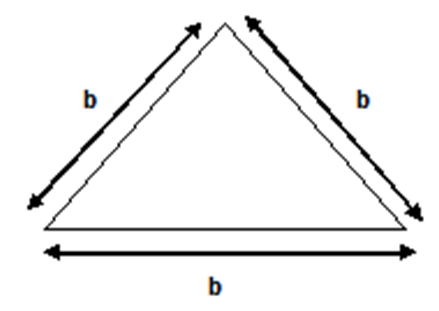
As we all know that, the  above picture or diagram is of a Triangle and in Triangle, all sides may be equal or may not be equal in length. Here ‘b’ defines each side of this Triangle, therefore perimeter of a Triangle is.  

Perimeter of a Triangle =  Sum of its 3 sides

                          =  b + b + b 

The Perimeter of a Triangle is the sum of the measure of the 3 sides.

AREA –   The area of a given figure is defined as the amount of surface covered by a figure. The area is always measured in square unit.

RECTANGLE -

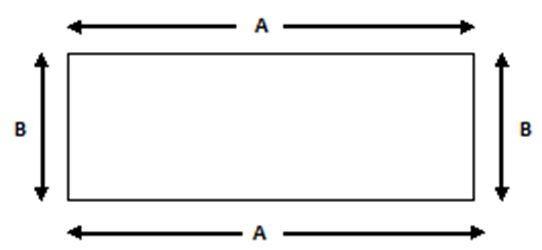
The above picture or diagram is of Rectangle and in Rectangle there are two opposite sides that are equal in length and width. Here ‘A’ defines the length and ‘B’ defines the width of this rectangle.

The area of a Rectangle is to be described by multiplication of Length and Width of a Rectangle and the unit should be measured by the square unit.

Area of a Rectangle =  A x B = AB

Unit used for the measurement of Area -

1)  Small surface area is measured as square millimeter (mm²), square centimeter (cm²), square decimeter (dm²).

2)  Large surface area is measured as square meter (m²), square decameter (dam²), square hectometer (hm²).

3)  More than large surface are described as square kilometer (km²)    

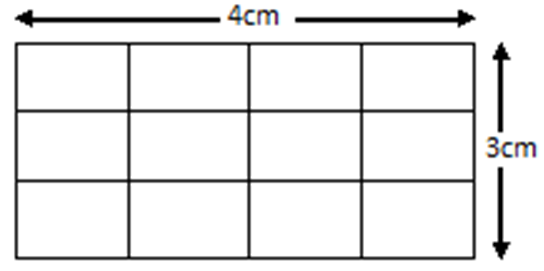
Above the picture you can observe that, there is a rectangle with 4 cm length and 3 cm width, and this rectangle has been divided into 12 no.s blocks of the  square. Suppose the area of each square is 1 cm² (sq cm)

Area of rectangle = Length x Width

                    = 4 x 3 = 12 sq cm (cm²)  [ as per formula ]

                    = number of unit squares in the rectangle

We can observe from the above rectangle figure-

The number of square along the length is 4 no.s and the number of square along the width is 3 no.s

If we multiply the square block number obtained from rectangle length & width wise , then 3 x 4 = 12 no.s square blocks. So, the area of each square block is = 12 sq cm (cm²) / 12 blocks

                 =  1 sq cm (cm²) / 1 block .

So, the area of each square block is 1 sq cm (cm²).

SQUARE

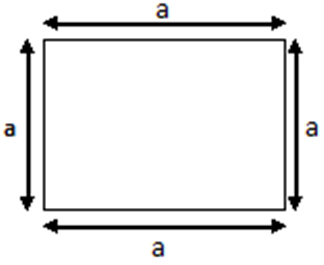
As we all know that, a square is a type of rectangle where all sides are equal.

So, the area of a square is

= one side (length) x another side (width)

= a x a =  a²

TRIANGLE 

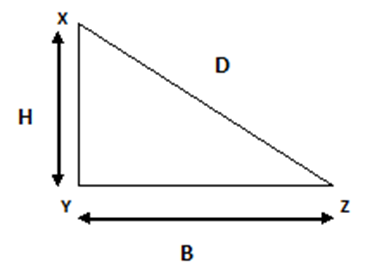
From the above shape, you can observe that there is a triangle with height ‘H’ and base ‘B’.

 XY = Height = ‘H’, 

 YZ = Base = ‘B’,

 XZ = Diagonal = ‘D’

 So, the area of a triangle is

= 1/2 x Base x Height 

= 1/2 x B x H

On the other way, we can use the area of a rectangle to find the area of the triangle

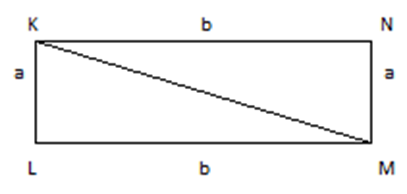
From the above picture we can observe the diagram of a Rectangle KLMN, between rectangle draw diagonal KM, Now we have two congruent right angle KLM & MNK

For Rectangle , KN = LM = b and  KL = NM = a

So, the area of the rectangle = Length x Width

               = KL x KN  or  LM x NM  or  NM x KN  or  KL x LM

                                                                            = a x b

Now, the area of Triangle = 1/2  x area of Rectangle

                              =  1 / 2 x a x b = 1/2 ab      

And the Diagonal of any ‘Rectangle’ is = √ (Length)² + (Width)²

                                          =  √ a² + b²

VOLUME –

The amount of space taken by a solid is known as it’s volume

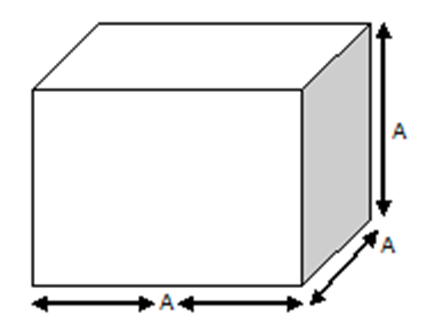
As we all know, the above picture or diagram is of the cube.

In every cube, there are Length, Height and Width

As we know that, every side of Cube is equal to each other. So, If Height is ‘A’, then Width is ‘A’ and Length is ‘A’, then the volume of cube must be –

        Volume of Cube =  Length x Width x Height

                          =  A x A x A

                          =  A³

Unit used for the measurement of Volume-

1)  Small covered area is measured as cubic millimeter (mm³), cubic centimeter (cm³), cubic decimeter (dm³).

2)  Large covered area is measured as cubic meter (m³), cubic decameter (dam³), cubic hectometer (hm³).

3)  More than large covered are described as cubic kilometer (km³).