CLASS-5
ARRANGING FRACTION DESCENDING ORDER
ARRANGING FRACTION DESCENDING ORDER -
To arrange fractions in descending order, we need to compare their values and sort them from highest to lowest. Here's how you can do it:
- Convert all fractions to equivalent fractions with a common denominator.
- Compare the numerators of the fractions.
- Sort the fractions based on the size of their numerators, from largest to smallest.
- If two or more fractions have the same numerator, compare their denominators and arrange them from smallest to largest.
- Write the fractions in descending order based on the sorted list.
For example, let's say we want to arrange the following fractions in descending order:
1/3, 2/5, 7/10, 1/2
- Find the common denominator: The smallest number that is divisible by all the denominators is 30. So, we'll convert each fraction to an equivalent fraction with a denominator of 30.
1/3 = 10/30 2/5 = 12/30 7/10 = 21/30 1/2 = 15/30
- Compare the numerators:
21/30 > 15/30 > 12/30 > 10/30
- Sort the fractions based on the size of their numerators, from largest to smallest:
21/30, 15/30, 12/30, 10/30
- If two or more fractions have the same numerator, compare their denominators and arrange them from smallest to largest:
21/30, 15/30, 12/30, 10/30
- Write the fractions in descending order based on the sorted list:
21/30 > 15/30 > 12/30 > 10/30
So, the fractions in descending order are:
7/10 > 1/2 > 2/5 > 1/3
To arrange fractions in descending order, you need to compare their values and order them from largest to smallest. Here's how you can do it:
- Find a common denominator for all the fractions. This will make it easier to compare their values. To find a common denominator, you can multiply the denominators of all the fractions together.
- Convert each fraction to an equivalent fraction with the common denominator. To do this, multiply the numerator and denominator of each fraction by the same factor.
- Once you have the fractions with the same denominator, you can compare their numerators. The fraction with the largest numerator is the largest fraction, and the fraction with the smallest numerator is the smallest fraction.
- Write the fractions in descending order, from largest to smallest.
In a quick understanding we can deliver or say that -
First find the L.C.M. Then form equivalent fractions such that the denominators are equal to the L.C.M. Then write in descending order comparing the numerators.
Example.1) Arrange the following fractions in descending order (use > sign):
1 7 5
-------, -------, --------
4 12 16
Ans.) Now, we would like to find the LCM of all the denominator of given fraction, and then we will divide obtained LCM by every denominator of given fraction one by one and then will multiply numerator and denominator by obtained quotient and make equalize all the denominator of the given fraction.
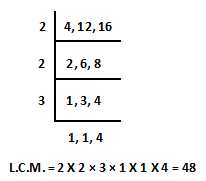
1 7 × 12 84
------- = ---------- = -------- [48 (LCM) ÷ 4 = 12]
4 4 × 12 48
7 7 × 4 28
------- = --------- = --------- [48 (LCM) ÷ 12 = 4]
12 12 × 4 48
5 5 × 3 15
------- = --------- = -------- [48 (LCM) ÷ 16 = 3]
16 16 × 3 48
84 28 15
------- > ------- > -------
48 48 48
(as 84 > 28 < 15)
The fractions arranged in descending order :
1 7 5
------- > ------- > -------- (Ans.)
4 12 16
Example.2) Arrange the following fractions in descending order (use > sign):
1 7 5
-------, -------, --------
15 5 30
Ans.) Now, we would like to find the LCM of all the denominator of given fraction, and then we will divide obtained LCM by every denominator of given fraction one by one and then will multiply numerator and denominator by obtained quotient and make equalize all the denominator of the given fraction.
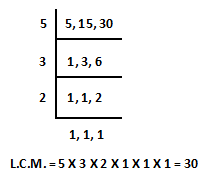
1 1 × 2 2
------- = ---------- = ------- [30 (LCM) ÷ 15 = 2]
15 15 × 2 30
7 7 × 6 42
------- = --------- = --------- [30 (LCM) ÷ 5 = 6]
5 5 × 6 30
5 5 × 1 5
------- = --------- = -------- [30 (LCM) ÷ 30 = 1]
30 30 × 1 30
42 5 2
------- > ------- > -------
30 30 30
(as 42 > 5 > 2)
The fractions arranged in descending order :
7 5 1
------- > ------- > -------- (Ans.)
5 30 15