CLASS-4
DIVISIBILITY - PROBLEM & SOLUTION

Example.2) Write the smallest number that should be (i) added to and (ii) subtracted from the following numbers to get them divisible by 6.

Ans.) (a)  81

(i) +3

3 should be added (81+3=84)

(ii) -3

3 should be subtracted (81-3=78)

EXPLANATION -

[Addition :-

It is not divisible by 2 as the last digit is not even (1).

If we add 1, it will be 82, but 8+2=10 which is not divisible by 3. 84 is the next even number, which is divisible both by 2 and 3.]

[For Subtraction :-

80 (not divisible by 3) and 79 (not divisible by 2).

But, 78 is divisible both by 2 and 3.]

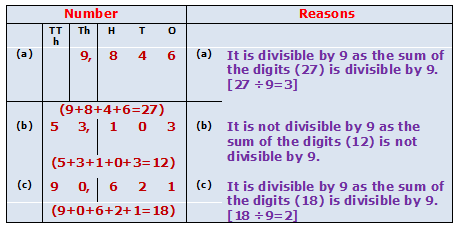
Example.3) Write whether the following numbers are divisible by 9 or not. Give reasons:

a) 9,846,          b) 53,103,        c) 90,621

Example.4) Write the smallest number that should be (i) added to and (ii) subtracted from the following numbers to get them divisible by 9.

(b) 277

(i) +2

2 should be added (277+2=279)

(ii) -7

7 should be subtracted (277-7=270)

EXPLANATION :-

[Addition :-

It is not divisible by 9 as the sum of digits is 16 (2+7+7=16). We know 18 is divisible by 9, we should add 2.

277+2 =279 is divisible by 9 (2+7+9=18). ]

[For Subtraction :-

2+7+7=16 is not divisible by 9.

16-7=9; 9 is divisible by 9.

We should subtract 7; 277-7=270

2+7+0=9; 270 is divisible by 9. ]

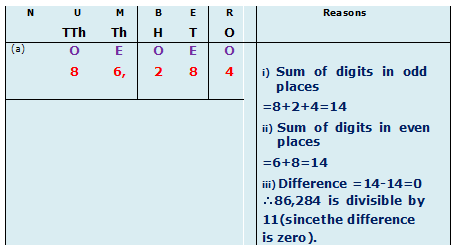
Example.5) Write whether the following numbers are divisible by 11 or not. Give reasons:          a. 86,284          b. 7,441

Ans.)

DIVISIBILITY BY 11 :-

EXPLANATION :-

Ø  Make a table as shown in example

Ø  First, mark the odd and even places alternately in the table as shown. The first place is always odd.

Ø  Find the sum of the digits that are in the odd places.

Ø  Next, find the sum of the digits that are in the even places.

Ø  Now, find the difference between these two sums (subtract).

Ø  If the difference is exactly divisible by 11, the given number is divisible by 11.

Ø  Or, if the difference is zero (0), the given number is divisible by 11.

Ø  Otherwise the given number is not divisible by 11.

We should find sums of the digits in both odd and even places and their difference)    [O=ODD PLACE ; E= EVEN PLACE]

Example.6) Write whether the following numbers are divisible by 12 or not. Give reasons.   a. 23,940        b. 78,618

Ans.)  DIVISIBILITY BY 12 :-

EXPLANATION :-

Ø  Make a table as shown in example

Ø  First, check divisibility by 3 - find the sum of the digits of the given number .

Ø  If the sum of the digits is divisible by 3, the given number is divisible by 3.

Ø  Next, check divisibility by 4 - underline the digits in the ones and tens places (i.e. the last two digits).

Ø  If the underlined last two digits can be divided by 4 leaving no remainder, the given number is divisible by 4.

Ø  OR, if the underlined last two digits are both zeroes (00), the given number is divisible by 4.

Ø  If the number is divisible both by 3 and 4, then the given number is divisible by 12.

Ø  But, if the number is divisible by any one (either 3 or 4) or none, then the given number is not divisible by 12.

CHECK DIVISIBILITY BY 3 and 4 BOTH