CLASS-4
LEAST COMMON MULTIPLE (LCM)
LEAST COMMON MULTIPLE (LCM)
Any number can be a multiple of two or more numbers. Suppose there are two numbers these are 2 and 4.
To find any number of common multiple of the given numbers we should have to find the first common multiple and then multiply it 1 time, 2 times, 3 times.
Product of 2 & 4 is = 2 X 4 = 8.
Thus, the common multiples of 2 & 4 are – 8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40, …………
So, 8 is the LCM of 2 & 4.
Write the 5 common multiple of the following numbers
Example.1) 3 & 7
Ans.) Product of 3 & 7 is = 3 X 7 = 21
5 common multiplies of the following multiplies are = 21 x 1 = 21
21 x 2 = 42
21 x 3 = 63
21 x 4 = 84
21 x 5 = 105
So, LCM of the number 3 & 7 is 21 and first five multiples are 21, 42, 63 , 84, 105.
Example.2) 5 & 6
Ans.) Product of 5 & 6 is = 5 X 6 = 30
5 common multiples of the following multiplies are = 30 x 1 = 30
30 x 2 = 60
30 x 3 = 90
30 x 4 = 120
30 x 5 = 150.
So, LCM of the number 5 & 6 is 30 and the first five multiples are 30, 60, 30, 120, 150.
DIVISIBILITY -
Now we will learn, how to understand which ‘Dividend’ is divisible by which ‘ Divisor’.
Suppose there is a number, that is 453 and we have to find which number will be ‘Divisor’,
Firstly add all the digit of 453 like = 4 + 5 + 3 = 12 , 12 is divisible by 3
BASIC FACTORIZATION -
Basic Factorization is nothing but a simplified multiplication form.
For an example, basic factorization of 24 = 1 x 2 x 2 x 2 x 3.
basic factorization of 36 = 1 x 2 x 2 x 3 x 3.
a) 1 has only one factor and that is the number(1) itself. It is called ‘Unique‘ number.
b) 2, 3, 5, 7, 11, 13 have only two factors, 1 and the number itself, these numbers are called ‘ Prime’ Numbers.
c) Numbers having three or more factor like 4, 6, 8, 10, 12, ……… are called ‘Composite’ Number.
LCM BY BASIC FACTORIZATION THROUGH DIVISION METHOD –
Example.1) Find the Basic Factors of the number 50 -
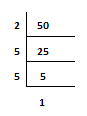
Step.1) First, consider 50 as dividend and consider the lowest number which is 2 which is count as ‘Divisor’. 50 ÷ 2 = 25. So, 25 is a ‘Quotient’.
Step.2) Put 25 below the position of 50 and then try to divide. We can find 5 is the lowest ‘Divisor’ for dividing the ‘Dividend’ 25 and we can get 5 as ‘Quotient’.
Step.3) Put 5 below the position of 25 and then try to divide. We can find 5 is the lowest ‘Divisor’ for dividing the ‘Dividend’ 5 and we can get 1 as ‘Quotient’.
So, basic factorization of 50 is 2 x 5 x 5 x 1 (Ans.)
Example.2) Find the Basic Factors of the number 80 -
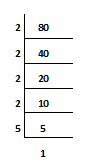
Step.1) First, consider 80 as dividend and we can find the lowest number which is 2 and 2 will be considered as ‘Divisor’. 80 ÷ 2 = 40. So, 40 is a ‘Quotient’.
Step.2) Put 40 below the position of 80 and then try to divide. We can find 2 is the lowest ‘Divisor’ for dividing the ‘Dividend’ 40 and we can get 20 as ‘Quotient’ .
Step.3) Put 20 below the position of 40 and then try to divide. We can find 2 is the lowest ‘Divisor’ for dividing the ‘Dividend’ 20 and we can get 10 as ‘Quotient’
Step.4) Put 10 below the position of 20 and then try to divide. We can find 2 is the lowest ‘Divisor’ for dividing the ‘Dividend’ 10 and we can get 5 as ‘Quotient’
Step.5) Put 5 below the position of 10 and then try to divide. We can find 5 is the lowest ‘Divisor’ for dividing the ‘Dividend’ 5 and we can get 1 as ‘Quotient’.
So, basic factorization of 80 is 2 x 2 x 2 x 2 x 5 x 1 (Ans.)
Example.3) Find the Basic Factors of the number 45 & 30 -

Step.1) First, consider 45 & 30 together as ‘Dividend’ and we can find the lowest number which is 5, and 5 is the common ‘Divisor’ of both the number 45 & 30. If 5 is ‘Divisor’ then, 45 ÷ 5 = 9 is ‘Quotient’ & 30 ÷ 5 = 6 is ‘Quotient’.
Step.2) Now put 9 & 6 below the number 45 & 30 respectively. Consider 9 & 6 as ‘Dividend’ and find the lowest common ‘Divisor’ for both the number 9 & 6. We can find, 3 is the lowest common ‘Divisor’ for dividing both the ‘Dividend’ 9 & 6, we can get 9 ÷ 3 = 3 & 6 ÷ 3 = 2, 3 & 2 as ‘Quotient’
Step.3) Now put 3 & 2 below the number 9 & 6 respectively. Consider 3 & 2 as ‘Dividend’ and find the lowest common ‘Divisor’ for both the number 3 & 2. We can find, 1 is the only lowest common ‘Divisor’ for dividing both the ‘Dividend’ 9 & 6 we can get 3 ÷ 1 = 3 & 2 ÷ 1 = 2, 3 & 2 as ‘Quotient’
So, LCM by basic factorization of 45 & 30 is 5 x 3 x 1 x 3 x 2 = 90.
(Ans.)
Example.4) Find the Basic Factors of the number 24 & 36 -

Step.1) First, consider 24 & 36 together as ‘Dividend’ and we can find the lowest number which is 2, and 2 is common ‘Divisor’ of both the number 24 & 36. If 2 is ‘Divisor’ then, 24 ÷ 2 = 12 is ‘Quotient’ & 36 ÷ 2 = 18 is ‘Quotient’.
Step.2) Now put 12 & 18 below the number 24 & 36 respectively. Consider 12 & 18 as ‘Dividend’ and find the lowest common ‘Divisor’ for both the number 12 & 18.
We can find, 2 is the lowest common ‘Divisor’ for dividing both the ‘Dividend’ 12 & 18. we can get 12 ÷ 2 = 6 & 18 ÷ 2 = 9, so respectively 6 & 9 is ‘Quotient’
Step.3) Now put 6 & 9 below the number 12 & 18 respectively. Consider 6 & 9 as ‘Dividend’ and find the lowest common ‘Divisor’ for both the numbers 6 & 9. We can find, 3 is the only lowest common ‘Divisor’ for dividing both the ‘Dividend’ 6 & 9. we can get 6 ÷ 3 = 2 & 9 ÷ 3 = 3. so respectively 2 & 3 is ‘Quotient’
Step.4) Now put 2 & 3 below the number 6 & 9 respectively. Consider 2 & 3 as ‘Dividend’ and find the lowest common ‘Divisor’ for both the number 2 & 3. We can find, 1 is the only lowest common ‘Divisor’ for dividing both the ‘Dividend’ 2 & 3. we can get 2 ÷ 1 = 2 & 3 ÷ 1 = 3. so, respectively 2 & 3 is ‘Quotient’
So, LCM by basic factorization of 24 & 36 is 2 x 2 x 3 x 1 x 2 x 3 = 72 (Ans.)
LCM by basic factorization -
Example.1) Find LCM of 15 & 25.

So, 15 = 3 x 5 x 1
25 = 5 x 5 x 1
In the above condition for both, the number of common factor is 5 & 1.
Now to find out the LCM of 15 & 25 multiply common factor 5 ,1 and uncommon factors 3 & 5.
So, product of the factors are = 3 x 5 x 5 x 1 = 75.
75 is the LCM of the 15 & 25. (Ans.)
There are some other way of solution of about Lowest Common Multiple (LCM) is given below for your more better understanding -
(i) Common Multiple Method Or Listing Method,
(ii) Common Division Method,
(iii) Prime Factorization Method,