CLASS-4
TRIANGLE

TRIANGLE -

A triangle is a closed geometric shape that consists of three straight sides and three angles. It is one of the basic shapes in geometry and is formed by connecting three non-collinear points in a plane. The sides of a triangle are the line segments that connect its three vertices, while its angles are formed by the intersection of two adjacent sides. The sum of the interior angles of a triangle is always 180 degrees, and the area of a triangle can be calculated using various formulas depending on the given information about its sides and angles. Triangles can be classified based on the length of their sides and the measure of their angles, and these classifications include equilateral, isosceles, scalene, acute, right, and obtuse triangles.

A triangle is a closed two-dimensional geometric shape that is formed by connecting three straight line segments or sides. Each side connects to another at a vertex, forming three angles at the vertices. The sum of the three interior angles of a triangle is always equal to 180 degrees. Triangles can have various classifications based on their sides and angles, such as equilateral (all sides and angles are equal), isosceles (two sides and two angles are equal), scalene (no sides or angles are equal), acute (all angles are less than 90 degrees), obtuse (one angle is greater than 90 degrees), or right (one angle is exactly 90 degrees). Triangles have a wide range of applications in mathematics, science, engineering, and many other fields.

A triangle is a geometric shape that is formed by three straight line segments that connect three non-collinear points. These three line segments are called the sides of the triangle, and the points where the sides meet are called the vertices of the triangle. The sum of the lengths of any two sides of a triangle is always greater than the length of the third side, a property known as the triangle inequality. Triangles are one of the most basic shapes in geometry, and they have a wide range of applications in fields such as mathematics, physics, engineering, and architecture.

A triangle is a three-sided polygon that is formed by connecting three non-collinear points in a plane. Each of the sides of a triangle is a line segment that connects two of the three vertices (points). The interior of a triangle is the region of the plane that is enclosed by the three sides. The angles of a triangle are the angles formed by the intersection of its sides. The sum of the angles in a triangle is always equal to 180 degrees. Triangles are a fundamental concept in geometry and have many important properties and applications in mathematics and other fields.

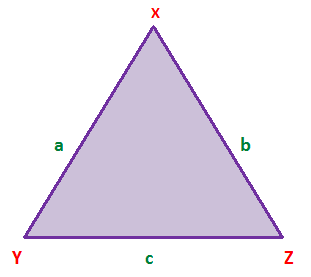
In above picture, ΔXYZ, XY = a, YZ = c, ZX = b

∠XYZ = ∠Y,

∠YZX = ∠Z,

∠ZXY = ∠X

Diagonal of a Triangle -

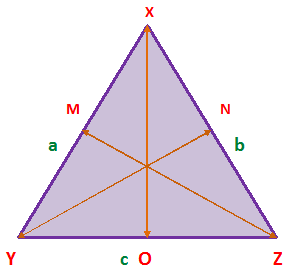
In above picture, ΔXYZ, diagonals are YN, ZM, XO

and, given XY = a, 

when,  XY = XM + YM     

  so,    XY = XM + XM   Or   XY = YM + YM    (where, XM = YM)

so,      XY = 2XM  Or,  XY = 2YM         

so,      XM = XY/2,  Or  YM = XY/2

so,      XM = a/2,   Or   YM = a/2       (given, XY = a)

Similarly, ZX = XN + ZN             (where, XN = ZN)

        then, XN = ZX/2 = b/2         (given, ZX = b)

         and, ZN = ZX/2 = b/2

Similarly, YZ = YO + ZO             (where, YO = ZO)

            then, YO = YZ/2 = c/2    (given, YZ = c)

             and, ZO = YZ/2 = c/2

Respective diagonals of the said triangle ΔXYZ are XO, YN, and ZM

As per the Pythagoras theorem -

       (XZ)² = (XO²+ ZO²)

=>     b² =  (XO)²+ (c/2)²

=>     (XO)² = b² - (c/2)² = (4b² - c²)/4

=>      XO = √(4b²- c²)/2 ..................(i)

     (XY)² = (YN)² + (XN)²

=>   a² = (YN)² + (b/2)²

=>   (YN)² = a² - (b/2)² = ( 4a² - b²)4

=>   YN = √(4a² - b²)/2 .................................(ii)

     (XZ)² = (ZM)² + (XM)² 

=>   b² = (ZM)² + (a/2)²

=>   (ZM)² = b² - (a/2)² = (4b²- a²)/4

=>    ZM = √(4b²- a²)/2 ............................(iii)