CLASS-4
LINE OF SYMMETRY
LINE OF SYMMETRY -
A line of symmetry is a line that divides a shape or object into two congruent parts that are mirror images of each other. In other words, if you were to fold the shape along the line of symmetry, the two halves would match up perfectly.
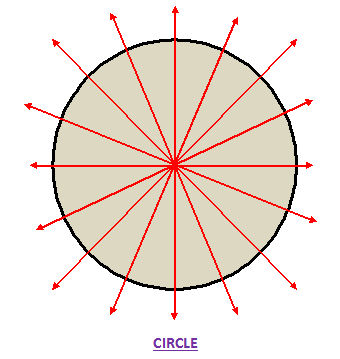
For example, a circle has an infinite number of lines of symmetry, since you can draw a line through the center of the circle and get two congruent halves. A square has four lines of symmetry - one through the middle of each side, and two diagonals. A rectangle has two lines of symmetry - one horizontal and one vertical, passing through the center of the rectangle.
Not all shapes have lines of symmetry, but many common geometric shapes do. Lines of symmetry can be useful for determining properties of a shape, such as its area or perimeter.
A line of symmetry is a line that divides a shape into two halves that are mirror images of each other. If you fold the shape along the line of symmetry, the two halves will match perfectly.
For example, a square has four lines of symmetry because it can be divided into four equal parts that are mirror images of each other. A circle has an infinite number of lines of symmetry because you can draw a line through the center of the circle in any direction and it will divide the circle into two halves that are identical.
Some other shapes and their lines of symmetry are:
- Triangle:- three lines of symmetry
- Rectangle:- two lines of symmetry
- Parallelogram:- zero lines of symmetry
- Regular pentagon:- five lines of symmetry
- Regular hexagon:- six lines of symmetry
Lines of symmetry are important in geometry and art because they help create balance and harmony in designs.
The line of symmetry produces reflections that coincide. Here’s how shapes and objects can have multiple lines of symmetry.


· The line of symmetry is also called the mirror line or axis of symmetry.
· A circle has infinite lines of symmetry.
Q. Draw the lines of symmetry for the following figures.
1. A rectangle has two lines of symmetry.

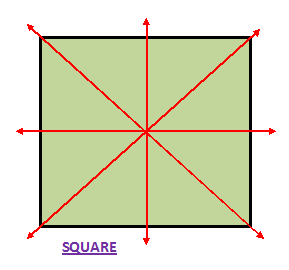
2. A square has four lines of symmetry.
3. An isosceles triangle has one line of symmetry.

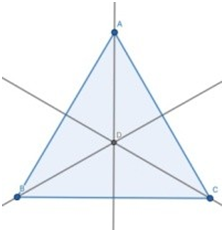
4. An equilateral triangle has three lines of symmetry.
5. A scalene triangle has no line of symmetry.

6. A circle has infinite (many) lines of symmetry.