CLASS-4
SQUARE

SQUARE -

A square is a geometric shape with four sides of equal length and four right angles. In other words, a square is a special type of rectangle where all sides are equal. A square can also be defined as a regular polygon with four sides, each of equal length and each angle measuring 90 degrees. The area of a square can be calculated by multiplying the length of one of its sides by itself, and the perimeter of a square can be calculated by adding the length of all four sides. Squares are often used in mathematics, geometry, and architecture due to their regular shape and symmetry.

A square is a geometric shape that has four equal sides and four equal angles (90 degrees each). It is a type of quadrilateral, which is a polygon with four sides. In a square, the opposite sides are parallel to each other and the diagonals bisect each other at right angles. The area of a square can be calculated by multiplying the length of one side by itself (squared), while the perimeter of a square is the sum of the lengths of all four sides. Squares are commonly used in mathematics, geometry, and construction, and are also a popular shape in art and design.

A square is a two-dimensional geometric shape with four equal sides and four right angles. Each of its sides is perpendicular to its adjacent sides, and its diagonals bisect each other at right angles. It is a special type of rectangle and a regular quadrilateral. The area of a square is calculated by multiplying the length of one of its sides by itself, while its perimeter is the sum of the lengths of all four sides. Squares are often used in mathematics, geometry, and engineering because of their symmetrical properties and ease of calculation.

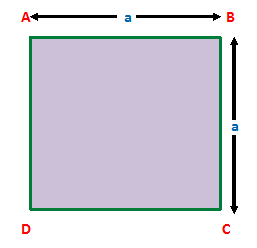
In above picture, the square has four equal sides -

AB = BC = CD = DA => a 

Now, the perimeter (P) of square = 4 X One side

                                     = 4 X a units = 4a units

Area (A) of the square = (side) X (side) square units

                          = (a X a) square units = a² units

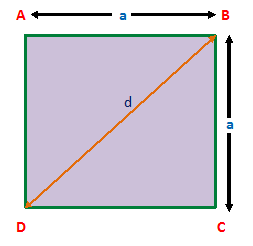
The every side of square is equal, AB = BC = CD =DA = a.

As per the Pythagoras theorem => BD² = AB² + DA²

                                        d² = a²+ a²

                                        d² =  2a²

                                        d = √2a² = a√2

so, the diagonal of a square is a√2 units