CLASS-4
ADDITION OF FRACTION

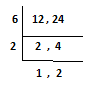
Step.1 - first find LCM of ‘Denominators’ 12 & 24.

 LCM = 6 x 2 x 2 = 24

So, LCM of 12 & 24 = 24,

 Put 24 as ‘Denominator’ at next step.                 

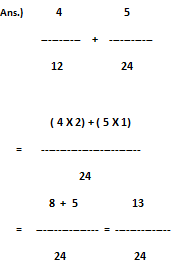
Step.2 – Divide by 'Denominator' of 1^st fraction to LCM, after getting the quotient from this divide, multiply it’s ‘Numerator’ & obtained quotient. 24 ÷ 12 = 2; 4 X 2 = 8.  So, 8 is the new ‘Numerator’ of 1^st fraction.

Step.3 – Divide by 'Denominator' of 2^nd fraction to LCM, after getting the quotient from this divide, multiply it’s ‘Numerator’ & obtained quotient. 24 ÷ 24 = 1 ;  5 X 1 = 5. So, 5 is the new ‘Numerator’ of 2^nd fraction

 Step.4 – Now, add two new ‘Numerators’ obtained from two separate. Fraction. 8 + 5 = 13 is new ‘Numerator’ .

        So, the answer is 13/24.    (Ans.)

 2)   3 / 12 + 2/6 + 3/18 =  ?

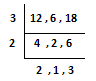
Step.1 - first find LCM of ‘Denominators’ 12, 6 & 18. 

LCM = 3 x 2 x 2 x 1 x 3 = 36

So, LCM of 12, 6 & 18 = 36, put 36 as ‘Denominator’ at next step.

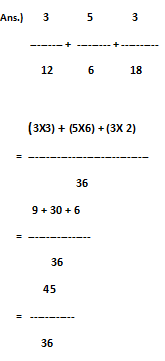
Step.2 – Divide by 'Denominator' of 1^st fraction to LCM, after getting quotient from this divide, multiply it’s ‘Numerator’ & earlier obtained quotient. 36 ÷ 12 = 3 ; 3 X 3 = 9. So, 9 is the new ‘Numerator’ of 1^st fraction. 

Step.3 – Divide by 'Denominator' of 2^nd fraction to LCM, after getting the quotient from this divide, multiply it’s ‘Numerator’ & earlier obtained quotient. 36 ÷ 6 = 6 ; 5 X 6 = 30. So, 30 is the new ‘Numerator’ of 2^nd fraction.

Step.4 – Divide by enominator of 3^rd  fraction to LCM, after getting the quotient from this divide, multiply it’s ‘Numerator’ & earlier obtained the quotient. 36 ÷ 18 = 2 ; 3 X 2 = 6. So, 6 is the new ‘Numerator’ of 3^rd fraction.

Step.5 – Now, add three new ‘Numerators’ obtained from three separate Fraction.  9 + 30 + 6 = 45 is the new ‘Numerator’ . 

So, the answer is  45/36.     (Ans.)