CLASS-11
SET BUILDER METHOD

SET BUILDER METHOD –

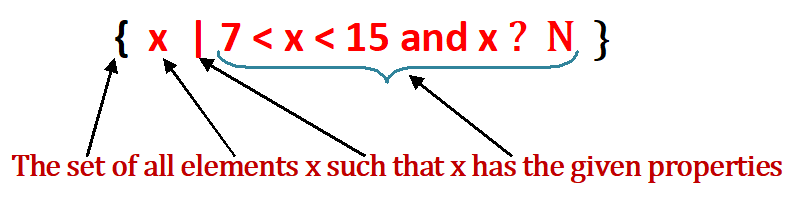
In this method a set is defined by stating properties which the statement of the set must satisfy. We use braces { } to write set in this form. The brace on the left is followed by a lower-case italic letter that represents any element of the given set. This letter is followed by a vertical bar and the brace on the right. Symbolically, it is of the form {x ǀ -}. Here we write the condition which ‘x’ satisfies, or more briefly, {x ǀ P(x)}, P(x) is a proposition stating a condition for x. The x is a sort of place holder, for all possible elements ‘x’ that have the given property. The vertical line is a symbol for ‘such that’ and the symbolic form A = {x ǀ x is even} reads “A is the set of numbers x such that ‘x’ is even. Sometimes a colon (:) or a semicolon (;) is also used in place of the vertical bar.”

                                  { x ǀ 7 < x < 15 and x ∈ N }

       The set of all elements x such that x has the given properties

Example.1) Write the following sets in the set builder form.

(a) The number 1, 3, 5,……….

Ans.)   {x ǀ x is an odd number}

(b) The solution of the equation x²+ 11x + 24 = 0

Ans.) {x : x² + 11x + 24 = 0}

               4          5          6          7          8         9

(c)  F = { -------, -------, -------, -------, -------, ------ }

               7          8          9         10         11        12

We observe that in the given set, the denominator of each fraction is 3 more than the numerator. Hence the set builder form of the set is -

                             n

        F  =  { x ǀ x = --------, n ∈ N and  4 ≤ x ≤ 9 }

                           n + 3

(d)   {0, 1, 16, 84, 256, 625, 1296}

Ans.)  We observe that the elements of the given set are the cubes of the first seven whole numbers. In the set builder form C = {x ǀ x = n⁴, n ∈ W and n ≤ 6}

Your second block of text...