CLASS-11
SETS - PROBLEM & SOLUTION

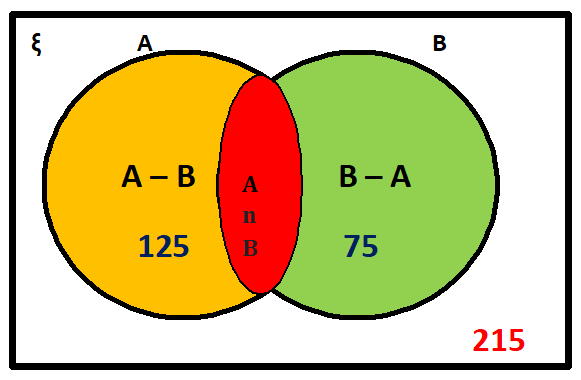
Given, n(ξ) = 750, n(A) = 450, n(B) = 400, and n(A ∩ B) = 325

n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 450 + 400 – 325 = 525

The given sets are intersecting sets. The Venn Diagram is as shown.

(ii) n(A ∪ B)’ = n(ξ) – n(A ∪ B) = 750 – 525 = 225

(iii) n(A – B) = n(A) – n(A ∩ B) = 450 – 325 = 125        (Ans.)

Example.2) Out of 100 candidates who appeared in an entrance exam test in English and Mathematics, 80 passed in at least one subject. If 60 passed in English and 65 in Mathematics, find –

(i) How many passed in both the subjects

(ii) How many passed in English only

(iii) How many failed in Mathematics

Ans.) Let, ξ be the set of all the candidates who took the test, A the set of candidates who passed in English and B of those who passed in Mathematics. Then –

Given, n(ξ) = 100, n(A ∪ B) = 80, n(A) = 60, n(B) = 65,

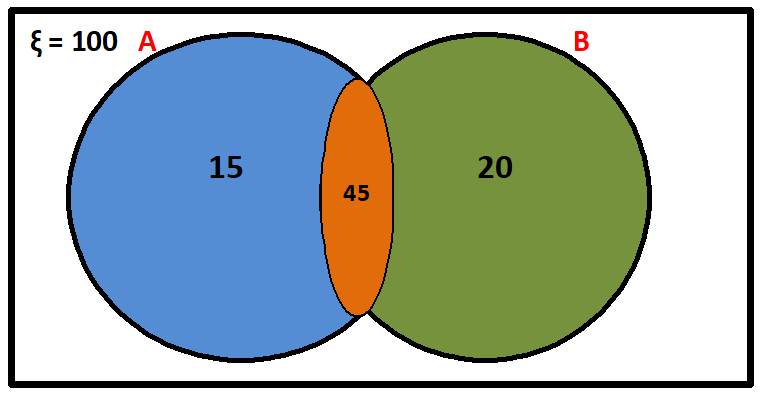
(i) n(A ∩ B) = n(A) + n(B) – n(A ∪ B) = 60 + 65 – 80  = 45

So, Number of candidates who passed in both the subjects = 45

(ii) Number of candidates who passed only in English

              = n(A – B)

              = n(A) – n(A ∩ B) = 60 – 45 = 15

(iii) Number of candidates who failed in Mathematics

              = n(B’) = n(ξ) – n(B)

              = 100 – 65 = 35                    (Ans.)

Example.3) 100 of the students at a language learning school take at least one of the languages French, German, and Russian, suppose 65 study French, 45 study German, 42 Study Russian, 20 study French and German, 25 study French and Russian and 15 Study German and Russian. Find the number of Students who study all the three languages.

Ans.) Let F, G, and R denotes the sets of studying French, German, and Russian respectively. Then –

n(F ∪ G ∪ R) = n(F) + n(G) + n(R) – n(F ∩ G) – n(F ∩ R) – n(G ∩ R) + n(F ∩ G ∩ R)

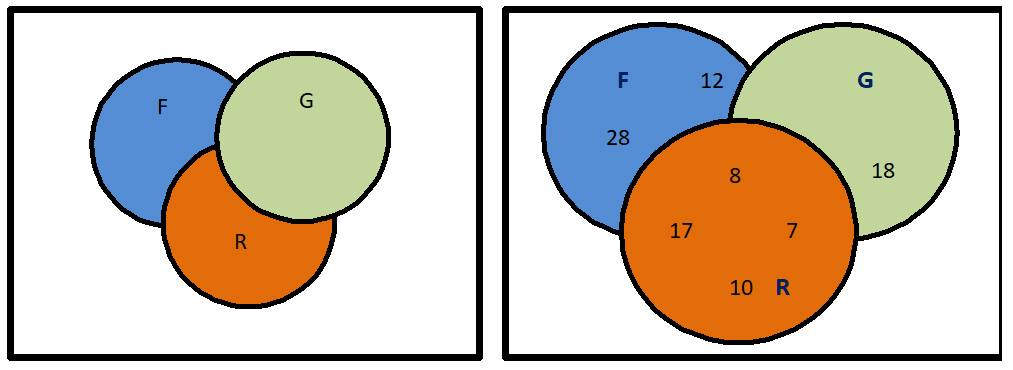
now, n(F ∪ G ∪ R) = 100, because 100 of the students study at least one of the languages in this school. n(F) = 65, n(G) = 45, n(R) = 42,

French + German = n(F ∩ G) = 20,

French + Russian = n(F ∩ R) = 25, and

German + Russian = n(G ∩ R) = 15.

So, n(F ∪ G ∪ R) = n(F) + n(G) + n(R) – n(F ∩ G) – n(F ∩ R) – n(G ∩ R) + n(F ∩ G ∩ R)

=>  100 = 65 + 45 + 42 – 20 – 25 – 15 + n(F ∩ G ∩ R)

=>  n(F ∩ G ∩ R) = 100 – 92 = 8

So, 8 students are there in these 100 students who are studying all three languages.

We may use this result to fill in the Venn Diagrams, we have –

8 study all three languages.

So,

=> 20 – 8 = 12 study French & German but not Russian,

=> 25 – 8 = 17 study French and Russian but not German,

=> 15 – 8 = 7 study German and Russian but not French.

Now,

=> 65 – 12 – 8 – 17 = 28 study only French,

=> 45 – 12 – 8 – 7 = 18 study only German,

=> 42 – 17 – 8 – 7 = 10 study only Russian.

120 – 100 = 20 do not study any of the languages

Thus, from the completed diagram, we can observe that 28 + 18 + 10 = 56 students study exactly one of the three languages.    (Ans.)