CLASS-11
SETS - INTERVAL
Intervals –
Many infinite sets, such as the real numbers, cannot be represented in roster form. There are other methods of representing these sets. For example, the number line represents the set of all real numbers.
The set of real numbers between 4 & 7, which is also an infinite set, can be represented on a number line or by an inequality.

An interval is the set of all numbers between two end points, such as 4 & 7.
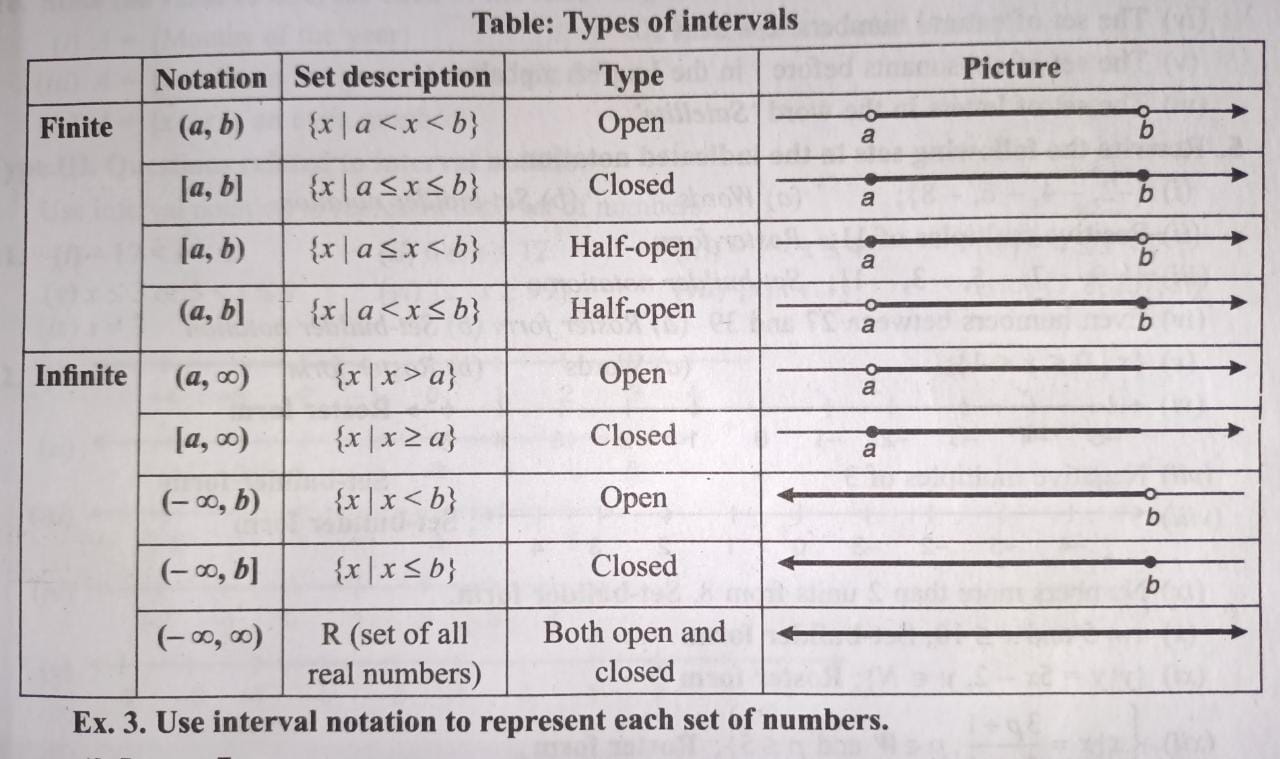
In Interval notation the symbols [and] are used to include an end point from an interval, and the symbols (and) are used to exclude an endpoint from an interval, e.g,
(4, 7) the set of real numbers between 4 and 7 but not including 4 & 7
The notation [ ] indicates closed interval as it includes the end points also while the notation ( ) is called an open interval as it does not include the endpoints of the interval
A finite interval is said to be closed if it contains both of its endpoints, half-open if it contains one endpoint but not the other, and open if it contains neither endpoint. The endpoints are also called boundary points when they make up the interval’s boundary. The remaining point of the interval are interior points and together comprise the interval’s interior. Infinite intervals are closed if they contains a finite end point, and open otherwise. The entire real line R is an infinite interval that is both open and closed.
An interval that extends forever in the positive direction goes to infinity (∞), and an interval that extends forever in the negative direction goes to negative infinity (- ∞).
There are some example are given blow for your better understanding –
1) Let, B = {3, 4, 5, 6, 7, 8}. Insert the appropriate symbol ∈ or ∉ in the blank spaces.
(i) 6…………B
Ans.) 6 ∈ B (because 6 belongs to set B)
(ii) 2…………….B
Ans.) 2 ∉ B (because 2 is not belongs to set B)
(iii) 4……………B
Ans.) 4 ∈ B (because 4 belongs to set B)
(iv) 10…………..B
Ans.) 10 ∉ B (because 10 is not belongs to set B)
Your second block of text...