CLASS-11
RELATION & FUNCTION - VERTICAL LINE TEST FOR A FUNCTION

Vertical Line Test For a Function –

You can test whether a given relation is a function or not by applying the following tests ,

(i) Examine whether the first set, i.e., the domain is fully used up or not

(ii) Examine whether the first members of all the ordered pairs are different or not. In an arrow diagram, examine whether each element of the first set has only one image in the second set or not.

(iii) The vertical line test. If it is possible to draw a vertical line that intersects the graph of a relation in more than one point, then the relation is not a function. If it is not possible to draw such a vertical line, then the relation is a function.

It is not difficult to read the theory behind this. If there are two points of the graph of a relation on a certain vertical line, then the two corresponding ordered pairs in the relation have the same first component but different second components. This means that the relation is not a function by the definition of a function.

Example.1) Which of the following relations are functions? Give reason. In case of a function, determine its domain and range.

(i) {(1, -2), (3, 7), (4, -6), (8, 11)}

(ii) {(1, 0), (1, -1), (2, 3), (4, 10)}

(iii) {(a, b), (b, c), (c, b), (d, c)}

Ans.) (i) and (iii) are functions because no two of their ordered pairs have the same first components; (ii) is not a function since the two ordered pairs (1, 0) and (1, -1) have the same first components.

Domain of (i) is {1, 3, 4, 8}. Range is {-2, 7, -6, 11}

Domain of (iii) is {a, b, c, d}. Range is {b, c}

Example.2) Which of the following relations are functions?

(i) y = 3x + 2

(ii) a is the capital of b where b ∈ B and B is the set of all countries, a ∈ A and A is the set of capital cities of countries

(iii) y < x + 3

(iv) y is the maths teacher of x where x represents any pupil taking up maths in a school

(v) y is a maths pupil of x, where x represents any math teacher in a school.

Ans.)  (i) Function. Each replacement of x gives one and only one replacement of y which makes the sentence true.

(ii) Function. Because normally each country has exactly one capital city.

(iii) Not a function. For each replacement of x there are many replacements of y which makes the sentence true.

(iv) Function. If we assumed that every pupils only one maths teacher.

(v) Not a Function. Each math teacher ordinarily has a number of pupils.

Example.3) State whether or not each of the following diagrams defines a function of  A = {a, b, c} into B = {x, y, z}

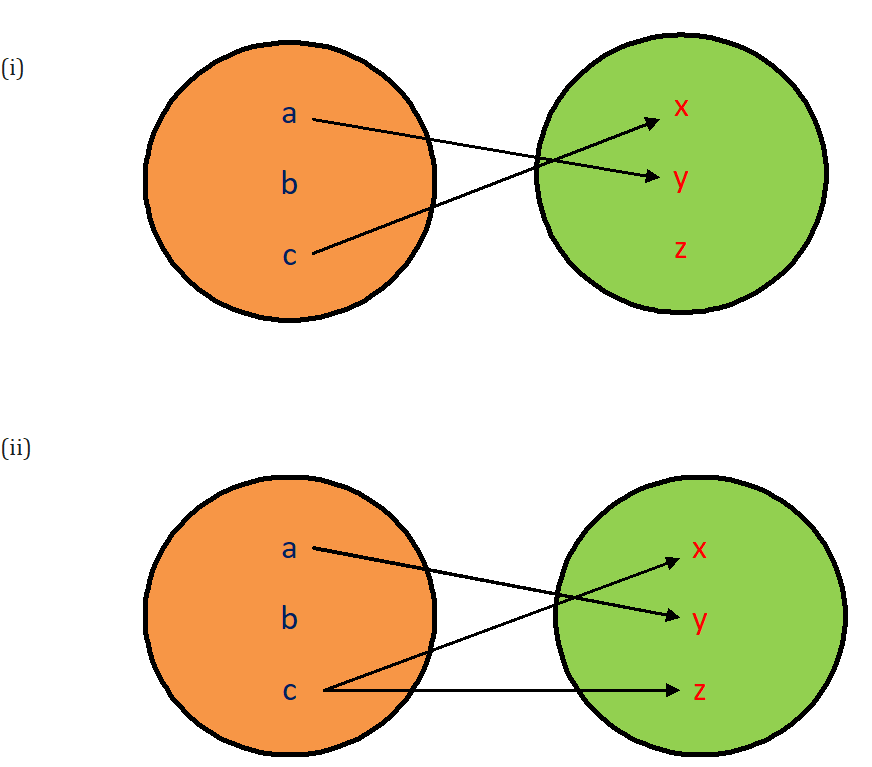
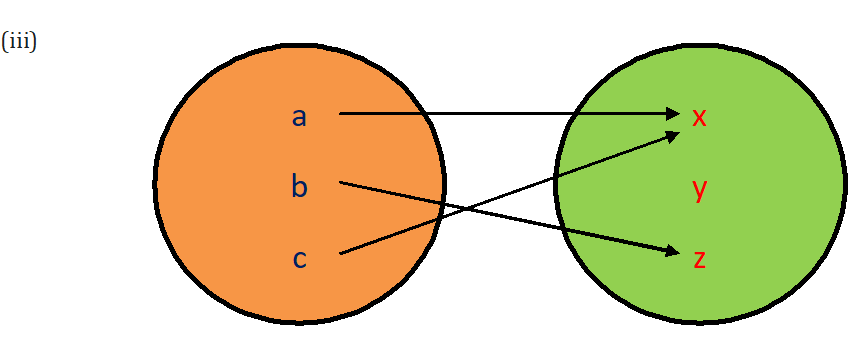
Ans.)  (i) No, the domain set A is not entirely used up.

(ii) No, two elements x & z are assigned to the same element c in the domain set A. This will yield ordered pairs (c, x), (c, z) having the same first component.

(iii) Yes, because a given association is a function even if (a) one element of the second set B is assigned to more than one element of the domain, (b) the second set B is not entirely used up.