CLASS-11
RELATION & FUNCTION - TYPES OF FUNCTION - ONE-ONE-ONTO FUNCTION-(BIJECTION)

One-One onto function (Bijection) –

If the function ‘f ’ is both one-one and onto, then it is called a one-one onto function. It is also called a bijection.

In other words, a function f : A → B is one-one onto if.

(i) It is one-one, i.e., f(x) = f(y)

                          =>  x = y for all x, y ∈ A

(ii) It is onto. i.e., for all y ∈ B, there exists x ∈ A such that f(x) = y

Note. If A and B are finite sets and f : A → B is a one-one onto function, then n(A) ≤ n(B) and n(B) ≤ n(A) => n(A) = n(B).

Illustrations –

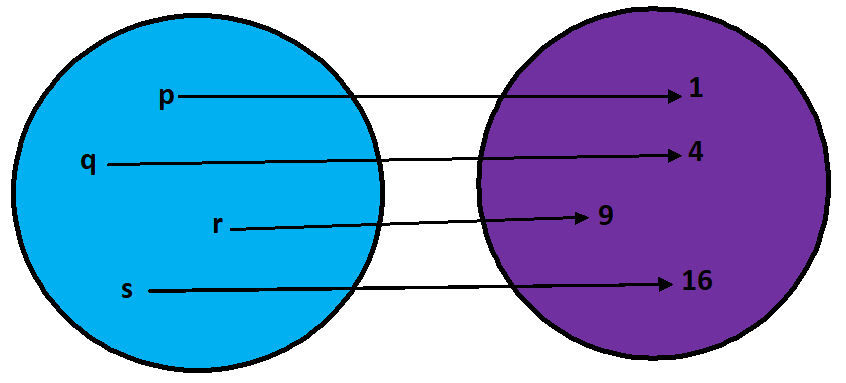
1) If A = {p, q, r, s}, and B = {1, 4, 9, 16} then f = {(p, 1), (q, 4), (r, 9), (s, 16)} is a one-one onto function.

2) Let, A = {a, b, c, d} and f : A → A, defined by  f(a) = e, f(b) = d, f(c) = b, f(d) = a, f(e) = c, then f is a bijection from A to A.

3) If R is the set of real numbers and Z the set of integers, then f : R → R defined by f(x) = x³ is a one-one onto function while f : Z → Z, f(x) = x³ is not a bijection. It is one-one but not onto since an element like-3 in co-domain Z has no pre-image in the domain Z.