CLASS-11
RELATION & FUNCTION - TYPES OF FUNCTION - MANY-ONE FUNCTION
Types Of Function- Many-One Function –
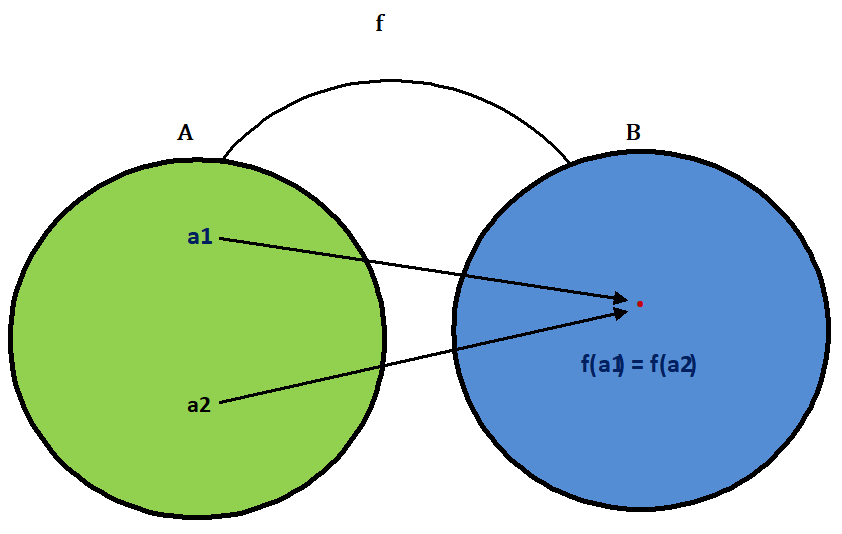
If the function f : A → B is such that two or more elements a₁, a₂,……………. of ‘A’ have the same f-image in ‘B’, then function is called many-one function.
Note that if the function f : A → B is not one-one, then f is many one.
Illustrations -
1) Let f : A → B be a function represented by the diagram shown in below figure.
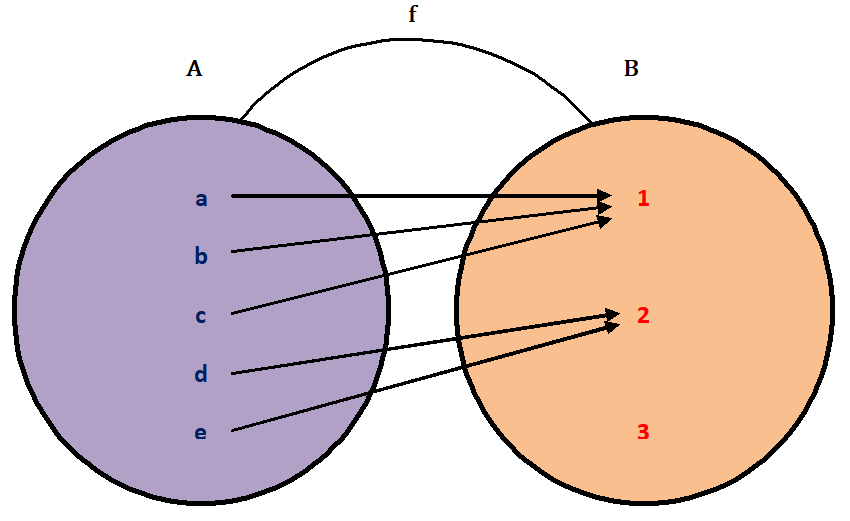
Clearly, f(a) = 1, f(b) = 1, f(c) = 1, f(d) = 2, f(e) = 2 and a ≠ b ≠ c, d ≠ e. So, f is a many-one function.
2) f : R → R, defined by f(x) = x²+ 5 is a many-one function, since f(- 1) = (- 1)² + 5 = 6
And f(1) = (1)² + 5 = 6, that is, two distinct elements – 1 and 1 have the same image is 6.
Example.1) Prove that the greatest integer function f : R → R, given by f(x) = [x] is a many-one function.
Ans.) The diagram shows that even though 1.3 ≠ 1.4 yet f(1.3) = f(1.4) = 1
Thus, two elements 1.3 and 1.4 in set A have the same image 1 in set B. Hence, f : A → B is not a one-one function. It is a many-one function.
Method to check whether the given function is Many-One -
Step.1) Consider any two arbitrary elements a₁, a₂ ∈ A
Step.2) Put f(a₁) = f(a₂) and solve the equation
Step.3) If we get a₁ ≠ a₂, then f is many-one.
Note. Recall that if we get a₁ = a₂, then f is a one-one function.
Onto function (Surjective Function) –
The mapping f : A → B is called an onto function if the set B is entirely used up, i.e., if every element of B is the image of at least one element of A.
=> for every b ∈ B there exists at least one element a ∈ A such that f(a) = b
=> Range of f is the co-domain of f (Range = Co-domain)
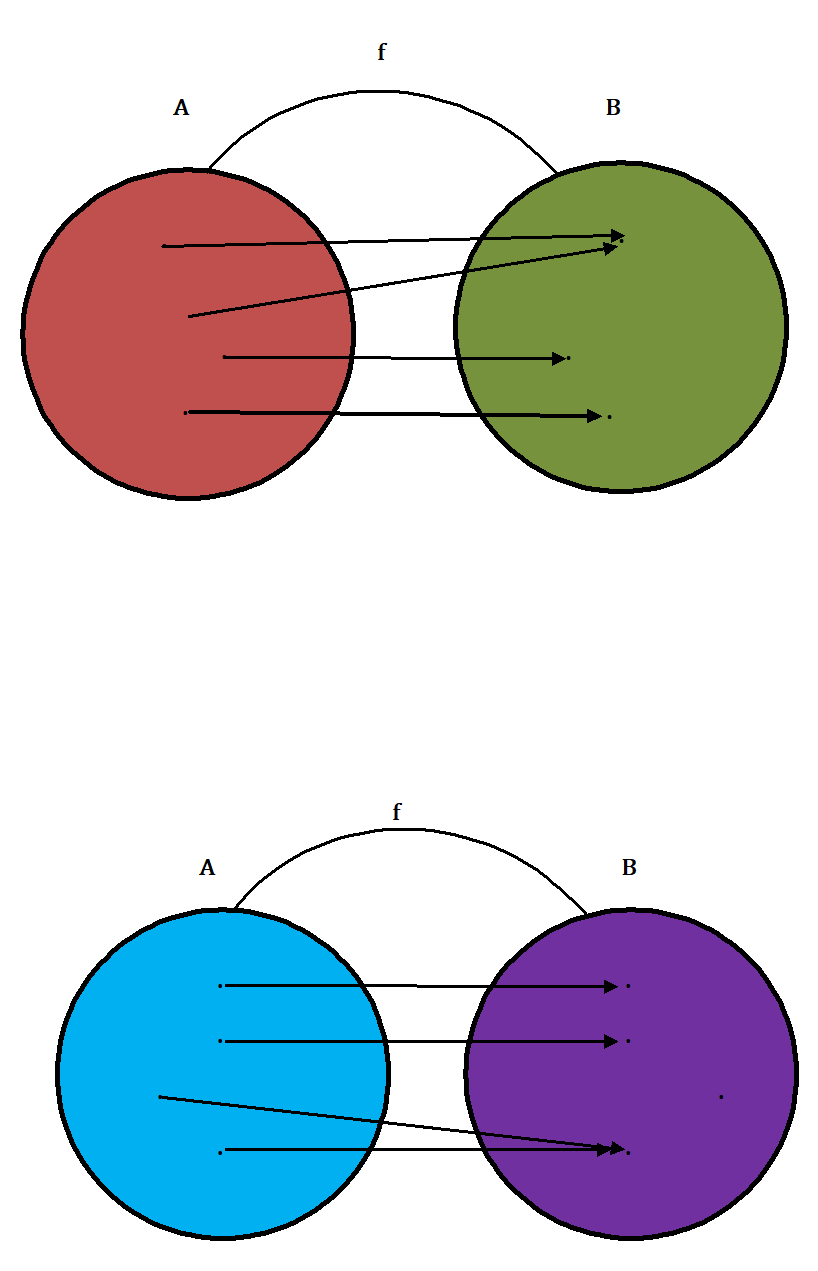
If function f : A → B is not onto, that is, some of the elements of B remain unmated, then ‘f’ is called an into function.
Remarks.1) An onto function is also called surjective function or a surjection.
Remarks.2) A one-one many-one function may be both onto and into.
Illustration –
1) Let A = {- 2, 2, - 3, 3}, B = {4, 9} and f : A → B be a functioned defined by f(x) = x², then f is onto, because f(- 2) = 4, f(2) = 4, f(- 3) = 9, f(3) = 9, i.e., f(A) = {4, 9} = B
Here, range = {4, 9} = B = co-domain.
2) A function f : N → N denoted by f(x) = 7x is not an onto function, because f(N) = {7, 14, 21,………..} ≠ N.
=> Range ≠ co-domain (N)
3) The function f : R → R defined by f(x) = ǀ x ǀ, x ∈ R is not onto since ǀ x ǀ is never negative and therefore no negative real number can be the image of any real number under ‘f’.
Here, also range = set of non-negative real numbers ≠ co-domain (R)
4) Consider the function f : R → R₁ defined by f(x) = √x², x ∈ R.
Let, x ∈ R₁, then x is non-negative real number,
So, √x² = x
=> f(x) = x,
Also, √(-x)² = √x² = x
=> f(-x) = x
Thus, all numbers in R (domain) have an image in R¹ (Co-domain), i.e., range (all numbers in R) = co-domain (R¹)
So, f is onto.
5) Let the function f : R → R be defined by the formula f(x) = x². The f is not an onto function since the negative numbers do not appear in the range of f, that is, no negative number is the square of a real number. Here, range of f ≠ R (co-domain). It is subset of R.
Example.1) Find whether the following are onto functions (surjections) or not
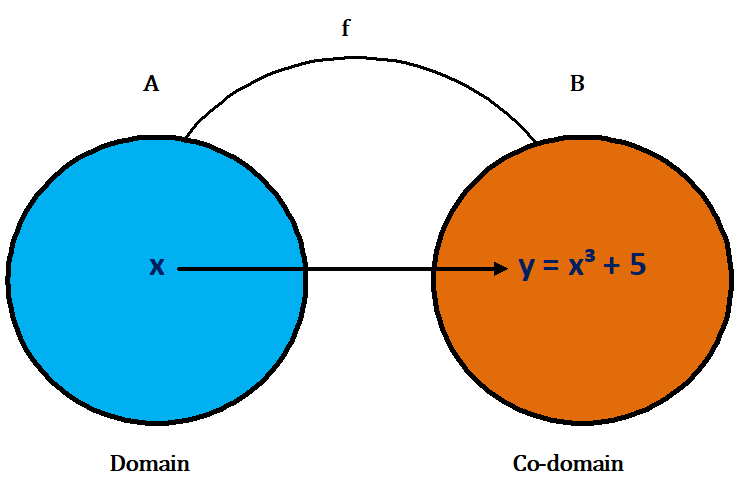
(i) f : R → R defined by f(x) = x³ + 5 for all x ∈ R.
(ii) f : R → R defined by f(x) = x² + 3 for all x ∈ R.
(iii) f : Z → Z defined by f(x) = 5x – 9 for all x ∈ Z.
Method –
Suppose f : A → B is a given function
Step.1) Choose any arbitrary element y in B.
Step.2) Put f(x) = y
Step.3) Solve the equation f(x) = y for x and obtained x in terms of ‘y’.
Let, x = g(y)
Step.4) If for all values of y ∈ B, the values of x obtained from x = g(y) are in A, then f is onto. If there are some y ∈ B for which x, given by x = g(y), is not in A, then ‘f’ is not onto.
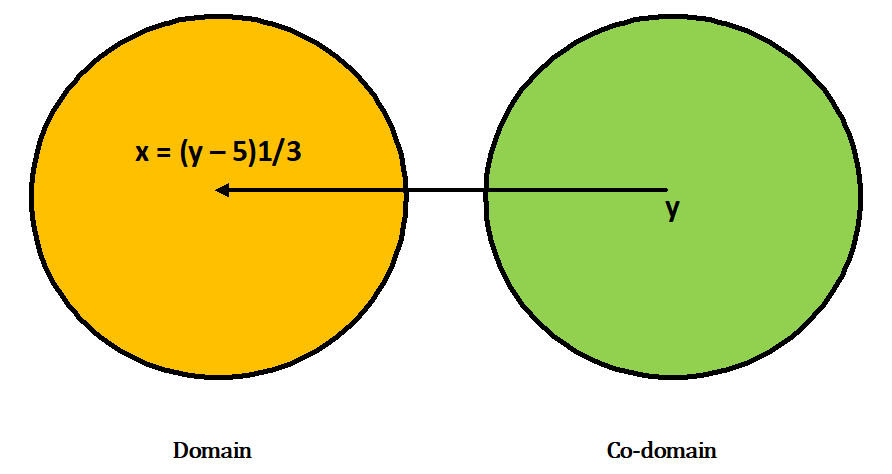
Ans.) Let there be an arbitrary element y in R. Then f(x) = y = x³ + 5
=> x³ = y – 5
=> x = (y – 5)⅓
Now, for all y ∈ R, (y – 5)⅓ is a real number. So, for all y ∈ R (co-domain), there exists
x = (y – 5)⅓. In R (domain) such that f(x) = x³ + 5
Here, f : R → R is an onto function.
(ii) f(x) = x² + 3 ≥ 3 for all x
∈ R. If we
take f(x) = a real number < 3, say = 2,
then x² + 3 = 2
=> x² = 3 – 2 = - 1 which is not true for any x ∈ R (domain).
So, 2 is not the image of any element in the domain.
So, ‘f ’ is not onto.
(iii) Let y be an arbitrary element of Z (co-domain). Then
f(x) = y = 3x + 2
(y – 2)
=> x = ----------
3
- 2
Now, if y = 0, then x = ------- ∉ Z. Thus, y = 0
3
in Z (co-domain) does not have its pre-image
in Z (domain).
Hence, f is not an onto function.