CLASS-11
THE NOTATION xRy

The Notation xRy –

If (x, y) is a member of a relation R, then we also use the symbolism ‘xRy’ and read ‘x is the relation R to y’.

(x, y) ∈ R => xRy

If, (x, y) ∉ R,

relation & function


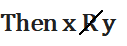
For example, for the relation ‘is the capital of’, we have ‘Beijing R China’, ‘Colombo R Sri-Lanka’, ‘Dhaka R Bangladesh’.  We give below more examples of relations which can be expressed via the ‘xRy’ symbolism.

(i) Let ‘R’ mean ‘is equal to’. Then ‘xRy’ means x = y

(ii) Let A = {2, 3, 4, 5,………….,12} and R means  ‘is one-third of’ in A X A,

then 2R6, 3R9, 4R12 =>  R = {(2, 6), (3, 9), (4, 12)}

Note.1) We emphasize that relations are sets and therefore any statements about sets or any operation defined on sets are appropriately applied to relations. One can thus speak of the intersection or union of two relations or speak of one relation being a subset of another.

Note.2) In the above picture , we have seen that the product set A X B is a set of ordered pairs (a ∈ A, b ∈ B). Since a relation is also a set of ordered pairs, therefore a relation is the subset of a product set.