CLASS-11
RELAION & FUNCTION - INVERSE OF A RELATION

The Inverse of a Relation –

For any binary relation R, a second relation can be constructed by merely interchanging first and second components in every ordered pair. The relation thus obtained is called the inverse of the first one and is designed by R‾¹. Symbolically –

                R‾¹ = {(y, x), (x, y) ∈ R} 

Thus, domain (R‾¹) = Range (R) and Range (R‾¹) = Domain (R)

Illustration.- 

(i) The inverse of the husband-wife relation is the wife husband relation.

(ii) Let, R = {(2, 1), (3, 2), (4, 3), (4, 5)}

Domain (R) = (2, 3, 4), Range (R) = {1, 2, 3, 5}

=> Domain (R‾¹) = Range (R) = {1, 2, 3, 5}, and

Range (R‾¹) = Domain (R) = {2, 3, 4}

Hence, R‾¹ = {(1, 2), (2, 3), (3, 4), (5, 4)}

(iii) If, R = {(x, y) ǀ x = y + 2} and S = {(x, y) ǀ y = x²} then

R‾¹ = {(x, y) ǀ y = x + 2} and S‾¹ = {(x, y) ǀ x = y²}

It can be easily shown that (R‾¹)‾¹ = R

Example.1) Let, R be the relation from A = {1, 2, 3, 4, 5, 6}, to B = {1, 3, 5} which is defined by the open sentence “x is less than y”

(i) Find the solution set R, that is, write R as a set of ordered pairs.

(ii) Plot R on a co-ordinate diagram of A X B.

(iii) State the domain, range and co-domain of R.

Ans.) 

(i) R consists of those ordered pairs (a, b) ∈ A X B for which a < b, hence

 R = {(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}

(ii) R is sketched on the co-ordinate diagram of A X B as shown in the figure

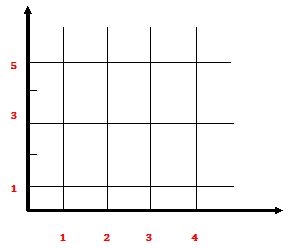
(iii) Domain of R = {1, 2, 3, 4}

        Range of R = {3, 5}

        Codomain of R = {1, 3, 5}

Example.2) Let A = {a, b, c, d} and B = {x, y, x}. Which of the following are relations from A to B ?

(i) {(a, y), (a, z), (c, x), (d, y)}

(ii) {(a, x), (b, y), (c, x), (a, d)}

(iii) {(a, x), (y, d), (x, c)}

(iv) {(y, a), (z, a), (z, c), (y, d)}

(v) {(a, x), (x, a), (b, y), (y, b)}

(vi) {(a, x), (b, y), (c, z), z}

(vii) {a, b, x, y, z}

Ans.) (i) Yes,

(ii) No, because in the ordered pair (a, d), a ∈ A and d ∉ B

(iii) No, because in (y, d), y ∈ B.

(iv) No, because here the first entries in all the ordered pairs are in the set B.

(v) No.

(vi) No, because the element z is not an ordered pair.

(vii) No, because the elements of the set are not ordered pairs.