CLASS-11
RELATION & FUNCTION - EXPONENTIAL FUNCTION
EXPONENTIAL FUNCTION -
The exponential function, denoted as eⁿ, is a fundamental mathematical function that arises naturally in many areas of mathematics, science, and engineering. It is defined as the function that raises the mathematical constant e (approximately equal to 2.71828) to the power of n:-
eⁿ
The exponential function has several key properties:
- Exponential Growth:- When n is positive, the function eⁿ grows rapidly as n increases. This property makes it useful for modeling processes that exhibit exponential growth, such as population growth, radioactive decay, and compound interest.
- Exponential Decay:- When n is negative, the function eⁿ decays rapidly towards zero as n decreases. This property is also widely used in modeling processes like radioactive decay and cooling of objects.
- Derivative Property:- The exponential function is its own derivative, meaning that the rate of change of eⁿ with respect to n is equal to eⁿ. In mathematical notation:
d
--------- eⁿ = eⁿ
dn
4. Multiplicative Property:- eᵐ X eⁿ = eᵐ⁺ⁿ. This property makes the exponential function useful in simplifying expressions involving exponents.
5. Inverse Function:- The natural logarithm function ln (n) is the inverse of the exponential function eⁿ. This means that ln (eⁿ) = n, and eˡⁿ⁽ⁿ⁾ = n for all appropriate values of n.
The exponential function has wide-ranging applications in mathematics, physics, engineering, economics, and many other fields. It provides a powerful tool for modeling growth and decay phenomena and solving differential equations.
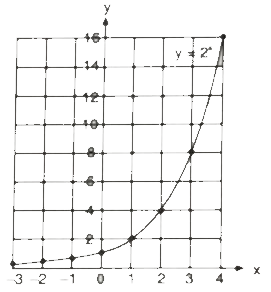
Example.1) Draw a graph of y = 2ⁿ
Ans.) Here, we see that as n ⟶ ∞, y ⟶ ∞ and when n ⟶ - ∞, y ⟶ 0
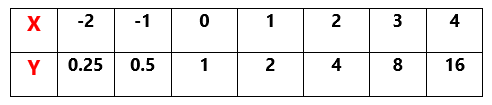
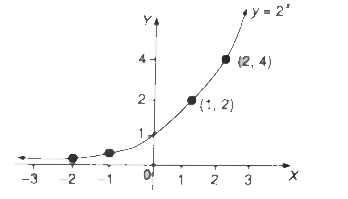
you can round 1/8 = 0.125 as 0.1 and 1/4 = 0.25 as 0.3 and draw the graph like above of y = 2ⁿ for -3 ≤ n ≤ 4 as shown below -

Any function of the form f(x) = aⁿ, where a > 0 and a ≠ 1, is called an exponential function with base a, The graph of the function has equation y = aⁿ.
Example.2) Draw the graph of y = aⁿ
Ans.) Before we draw the graph, we should keep in mind the following facts.
(a) logₐx is defined for positive values of x only and base a is always positive.
(b) For all values of a, logₐ1 = 0 since a⁰= 1.
(c) When a > 1, logₐ∞ = ∞, since a˄∞ = ∞, and logₐ0 = - ∞
since a˄∞ = ∞, and logₐ 0 = - ∞.
1 1
since a˄-∞ = ------ = ------ = 0
a˄∞ ∞
(d) When 0 < a < 1, logₐ∞ = -∞, since a˄-∞ = (1/a)˄∞ = ∞ as 1/a > 1 and logₐ0 = ∞, since
a˄∞ = (1/a)˄-∞ = 0 as 1/a > 1,
(e) For all positive values of a, aⁿ is positive, whether 'n' is positive or negative, and aⁿ never vanishes for finite values of n. Now we shall draw the graph of aⁿ, of y = aⁿ.
Case.1:- Let a > 1. y = aⁿ
(i) The curve does not pass through the origin.
(ii) It cuts the x-axis when y = 0, 0 = aⁿ only when x = - ∞.
The curve meets the negative direction of the x-axis at infinity, y ⟶ 0 as x ⟶ - ∞
(iii) It cuts the y-axis when n = 0
y = a⁰ = 1.
The curve meets the y-axis at (0, 1).
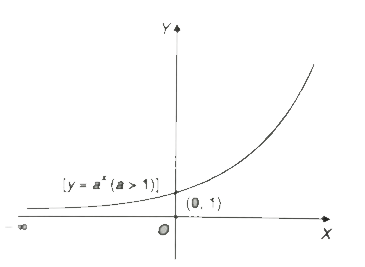
(iv) aⁿ, y is positive whether x is positive or negative. In other words, the curve lies only in the first and second quadrants, i.e., above the x-axis.
(v) As x increases, y increases, i.e., y is an increasing function of x. i.e., y ⟶ ∞ as x ⟶ ∞
Hence, the curve is drawn in above figure.
The above holds good for function eⁿ also e > 1.
Case.2:- Let, 0 < a < 1. y = aⁿ
(i) The curve does not pass through the origin.
(ii) It cuts the x-axis when y = 0, i.e., x = ∞
The curve meets the positive direction of the x-axis at infinity, i.e., y ⟶ 0 as x ⟶ ∞,
(iii) It cuts the y-axis when x = 0, i.e., y = 1.
The curve meets the y-axis at (0, 1)
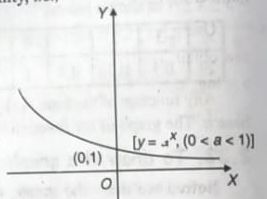
(iv) aⁿ is positive, whether n is positive or negative. In other words, the curve lies only in the first and the second quadrants, i.e., above the x axis.
(v) As x increase, y decrease, i.e., y is a decreasing function of n, i.e., y ⟶ 0 as x ⟶ ∞,
i.e., y ⟶ ∞ as x ⟶ - ∞