CLASS-11
RELATION & FUNCTION - EQUALITY OF ORDERED PAIRS
Equality of Ordered Pairs –
Two ordered pairs of numbers are defined to be equal when both the first components are equal and
9 16
also their second components are equal. Thus, (- 3, 4) = (- -----, -----)
3 4
but (4, 5) ≠ (5, 4),
(7, 9) ≠ (7, 5), (6, 11) ≠ (3, 11)
If A = {a, b}, then all possible ordered pairs are (a, a) (b, b) (a, b) (b, a).
If A = {a, b, c} and B = {1, 2, 3, 4}. Then all possible ordered pairs such that in each ordered pair the first component is an element of set A and second component is an element of set B are obtained by pairing each element from set A with each element from set B. This can be done by the following scheme –
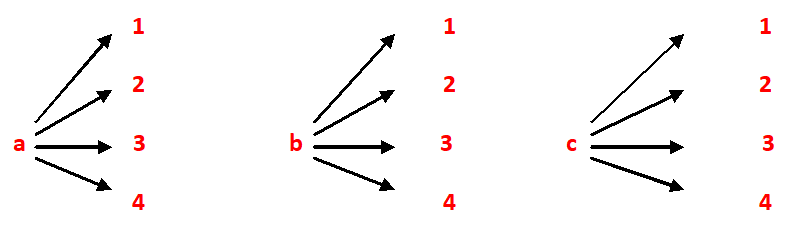
(a, 1), (a, 2), (a, 3), (a, 4), (b, 1), (b, 2), (b, 3), (b, 4), (c, 1), (c, 2), (c, 3), (c, 4)
Example.1) Express {(x, y) : x² + y² = 25, where x, y ∈ W} as a set of ordered pairs.
Ans.) Let us find possible values of whole numbers x, y which make x² + y² = 25.
x = 0, y = 5 => x² + y² = 0² + 5² = 25
x = 3, y = 4 => x² + y² = 3² + 4² = 25
x = 4, y = 3 => x² + y² = 4² + 3² = 25
x = 5, y = 0, => x² + y² = 5² + 0² = 25
so, the required set of ordered pairs is {(0, 5), (3, 4), (4, 3), (5, 0)}
Example.2) The number of elements in the set {(a, b) : 2a² + 3b² = 35, a, b ∈ Z}, where Z is the set of all integers is –
(a) 2 (b) 4 (c) 8 (d) 12
Ans.) Given set is {(a, b) : 2a² + 3b² = 35, a, b ∈ Z
By trial, we see that 2(±2)² + 3 (±3)² = 35, and 2(±4)² + 3(±1)² = 35
So, 8 elements of the sets are –
{(2, 3), (2, -3), (-2, 3), (-2, -3), (4, 1), (4, -1), (-4, 1), (-4, -1)}
Your second block of text...