CLASS-11
RELATION & FUNCTION - CLASSIFICATION OF FUNCTION - SPECIAL FUNCTION
CLASSIFICATION OF FUNCTION -
C) Special Functions –
1.) Constant Function.
If ‘k’ is a fixed real number, then, the functions f : R → R : f(x) = k for all x ∈ R is called the constant function.
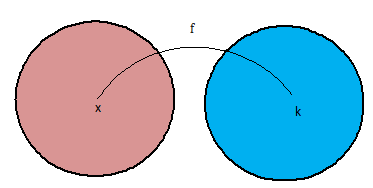
For the constant function f(x) = k ⩝ x ∈ R we have domain of f = R and range of f = {k}.
2.) Identity Function.
The identity function maps each number of the domain onto itself. That is, if I is the identity function, then for any ‘x’ in the domain, I(x) = x
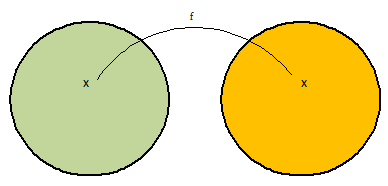
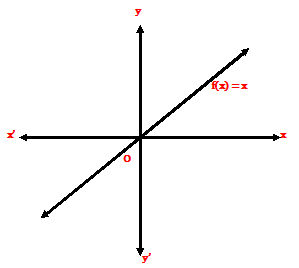
If we let y stand for I(x), then y = (x). It is easy to see that if the domain of ‘I’ is the set of real numbers, then the graph of the identity function is the y = x.
3.) Modulus Function.
The function defined by
x; when x ≥ 0
f(x) = ǀ x ǀ = {
- x; when x < 0
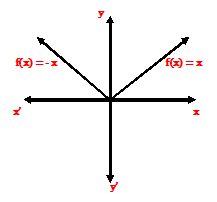
is called the modulus function.
For any real numbers x, we have √x² = ǀ x ǀ
4.) Greatest Integer Function.
The symbol [x] denotes the greatest integer less than or equal to x.
For example, [4] = 4, [4.1] = 4, [0] = 0, [- 1.3] = - 2, [π] = 3, [- π] = - 4
The function with equation y = [x] is called the greatest integer functions. This is an example of step function.
The graph of step function can be drawn as shown below. It is known as step graph because it increases or decrease in steps rather than being a continuous line
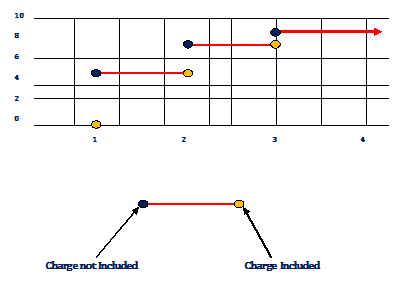
(i) What is the charge for parking for –
1
(a) 2 h (b) 2 ----- h (c) 3 h (d) 4 h
2
Ans.) (i) (a) Cost for 2 h parking = $ 6
1
(b) Cost for 2 ------ h parking = $ 10
2
(c) Cost for 3 h parking = $ 10
(d) Cost for 4 h parking = $ 12
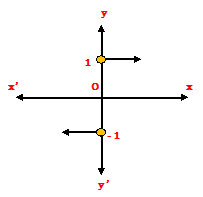
5) Signum Function –
The function f : R → R defined as,
ǀ x ǀ
------- for x ≠ 0,
x 1 if x > 0
f(x) = { , Sig x = { 0 if x = 0
0 for x = 0 - 1 if x < 0
Its domain is R and range is the set {- 1, 0, 1}.
6) Even & Odd Functions –
If f(x) is a function of x such that f(- x) = f(x) for every x of its domain, then it is called an even function of x. For example,
If, f(x) = cos (x) then f(- x) = cos (- x) = cos x so that f(x) = f(- x). Thus it is an even function. Similarity, y = x² + 7, y = cos 2x are also even functions.
If, f(x) is a function of x such that f(- x) = - (x) for every x of its domain, then it is called an odd function of x. For example,
If, f(x) = sin x, then f(- x) = sin (- x) = - sin x so that f(- x) = - f(x). Hence, f(x) is an odd function. Similarly, y = x²+ 6x, y = tan x are also odd functions.
Please Note. – There are functions which are neither even nor odd, e.g., y = x²- 3x + 1.