CLASS-11
RELATION & FUNCTION - ABSOLUTE VALUE FUNCTION

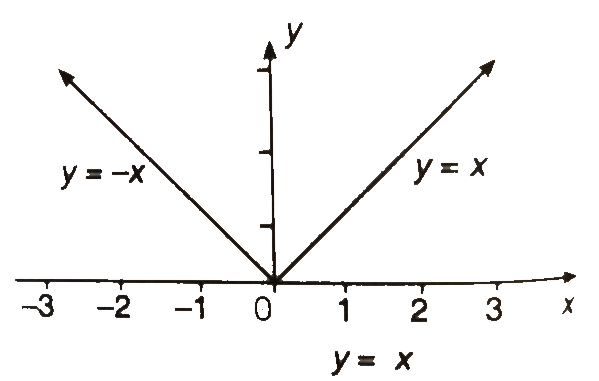
When x ≥ 0, y =│x│is equivalent to y = x, the equation of the straight line through the origin with slope 1. When x < 0, y =│x│is equivalent to y = -x, the equation of the straight line through the origin with slope -1.

Example.2) Draw the graph of the function f(x) = │x - 1│

Ans.) The domain is the set of all real numbers. The range is the set of all non-negative real numbers. 

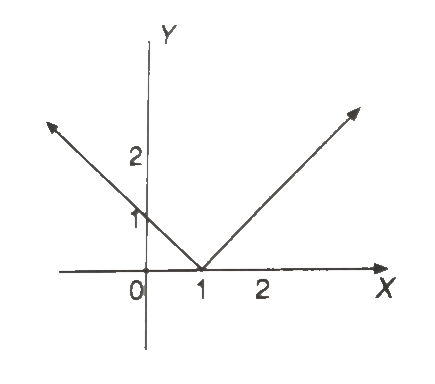
The graph is the graph of y =│x│ shifted one unit to the right. (Ans.)

Example.3) Draw the graph of the function f(x) = - x│x│.

Ans.) If x > 0, then y = f(x) = - x . x = - x²,

So, y = - x², for x > 0  ..........(i)

If, x = 0, then y = f(x) = 0,

So, y = f(x) = 0, for x = 0 ............(ii)

If, x < 0, then y = f(x) = (- x) (- x) = x², 

so, y = f(x) = x² for x < 0   .................(iii)

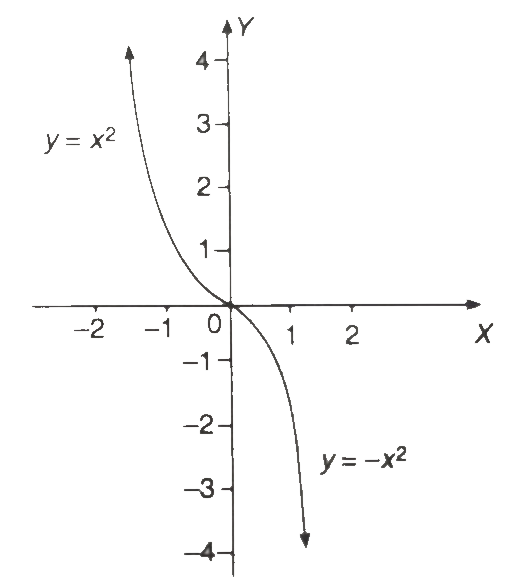
From (i), as x ⟶ ∞, y = - ∞ for x > 0.

From (iii), as x ⟶ - ∞, y ⟶ ∞ for x < 0,

From (ii), y = f(x) = 0 

Example.4) Draw the graph of the following functions

            │x│ 

(i) f(x) = ------,          (ii) f(x) = │x│+│x - 1│

              x

Ans.) (i) The domain is the set of all non-zero real numbers. The graph is the right half of the line y = 1 for x > 0, plus the left half of the line y = - 1 for x < 0. 

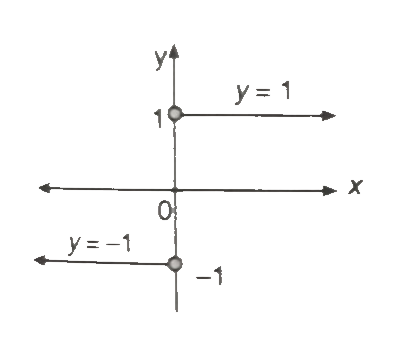
The range is {1, -1}. The graph is not defined for x = 0.

(ii) Case.1) x ≥ 1,  then f(x) = x + x - 1 = 2x - 1.

Case.2) 0 ≤ x < 1,  then f(x) = x - (x - 1) = 1.

Case.3) x < 0,   then f(x) = - x - (x - 1) = - 2x + 1.

So, the graph consists of a horizontal line segment and two half-lines.

Example.5) Draw the graph of the function y =│x - 2│+│x - 3│

Ans.) 

y = │x - 2│+│x - 3│

Here, we consider separate intervals.

When x > 3, (x - 2), (x - 3) both will be positive,

therefore,

y = x - 2 + x - 3

=> y = 2x - 5

Some points of the graph are -

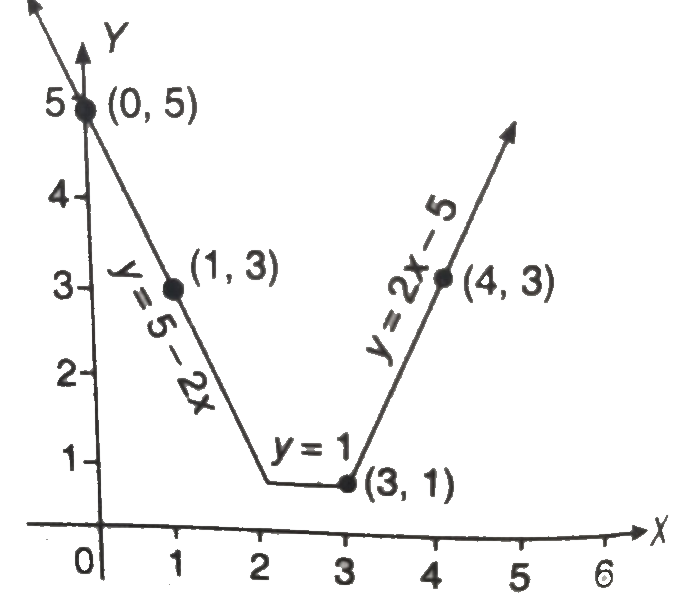
and if 2 < x < 3 then (x - 2) will be positive and (x - 3) will be negative, thus, 

             y = (x - 2) - (x - 3) = 1 

so, for 2 ≤ x ≤ 3, y = 1 (a line parallel to the x-axis)

Now, if x < 2, in this case both (x - 2) and (x - 3) will be negative and, therefore, y = - (x - 2) - (x - 3) = 5 - 2x.

Some points on the line y = 5 - 2x for x < 2 are -