CLASS-10
VOLUME & SURFACE AREA OF SOLIDS - CYLINDER
Volume & Surface Area of The Solids –
In this part we will be discussing about the volume and surface area of the Cylinder, Cone, and Sphere.Three dimensional solids – right circular cylinder, right circular cone, and sphere; Area (total surface and curved surface) and volume. Here we will learn, direct application problems including cost, inner and outer volume and melting and recasting method to find the volume or surface area of a new solid. Combination of solid included.
CYLINDER –
Solids like circular pillars, circular pipes, circular pencils, measuring jars, road rollers, and Gas cylinders etc. are said to be in cylindrical shape.
Formula for the volume and Surface Area of a Cylinder –
1) For a cylinder of base radius = r, and height = h, we have –
(i) Volume = πr²h cubic units
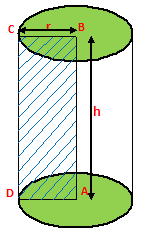
(ii) Curved surface area = 2πrh square units.
(iii) Total Surface area
= Curved Surface Area + Area of 2 Circular Ends
= 2πrh + 2πr²
= 2πr (h + r) sq.units
2) Hollow Cylinders –
Solid like iron pipes, rubber tubes, etc., are in the shape of hollow cylinders.
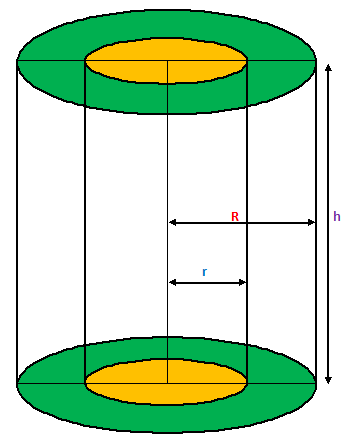
Consider a hollow cylinder of External Radius = R,
Internal Radius = r, and height = h. Then, we have
(i) Thickness of the Cylinder = (R – r)
(ii) Area of Cross Section = (πR²- πr²) = π(R²- r²) square unit.
(iii) Volume of material = External Volume – Internal volume
= πR²h - πr²h = πh(R²- r²) cubic units
(iv) Curved Surface Area = [External Curved Surface Area] + [Internal Curved Surface Area]
= (2πRh + 2πrh) = 2πh (R + r) square unit
(v) Total Surface Area = Curved Surface Area + 2(Area of Base Ring)
= {(2πRh + 2πrh) + 2(πR²- πr²)} square units
= 2π(Rh + rh + R²- r²) square units
There are some examples are given below for your better understanding -
Example.1) Find the (i) curved surface area, (ii) total surface area, and (iii) volume of a cylinder of diameter 8 cm and height 100 cm. Find its capacity in liters.
Ans.) As per the given condition –
Here, r = 8/2 cm = 4 cm, and h = 98 cm
According to the formulae -
(i) Curved Surface Area = 2πrh
22 8
= 2 X ------- X ------ X 98
7 2
= 22 X 8 X 14 = 2464 cm² (Ans.)
(ii) Total surface area = (2πrh + 2πr²) = 2πr (h + r)
22
= 2 X ------- X 4 X (98 + 4)
7
= 2 X 3.14 X 4 X 102
= 2562.24 cm² (Ans.)
(iii) Volume = πr²h
22
= ------- X 4² X 98
7
= 22 X 16 X 14 = 4928 cm³
4928
So, capacity of the cylinder = -------- = 4.928 liters (Ans.)
1000
Example.2) The total surface area of a cylinder of radius 5cm in 660 cm². Find the height of the cylinder.
Ans.) Let the height of the cylinder be ‘h’ cm, its radius, r = 5 cm
According to the formulae, Total surface area = 2πrh + 2πr²
= 2πr (h + r) sq.units
22
= 2 X ------- X 5 X (h + 5)
7
Now, as per the given condition –
22
=> 2 X ------- X 5 X (h + 5) cm² = 660 cm³
7
=> 220 (h + 5) = (660 X 7)cm
=> h + 5 = (3 X 7) cm
=> h = 21 – 5 = 16 cm
Hence the height of the cylinder is 16 cm. (Ans.)
Example.3) Diameter of a roller, 120 cm long, is 70 cm. If it takes 500 revolutions to level a playground, determine the cost of leveling it at the rate of $5 per square meter.
Ans.) Length of the roller, h = 120 cm, and its radius, r = 35 cm
Area covered by the roller in one revolution = curved surface area of the roller
= 2πrh
22
= 2 X ------- X 35 X 120
7
= (2 X 22 X 5 X 120) cm² = 26400 cm²
Now, as per the given condition, area covered by the roller in 500 revolutions
26400 X 500
= --------------- m²
100 X 100
= 1320 m²
So, cost of leveling the playground = $(1320 X 5) = $2700 (Ans.)
Your second block of text...