CLASS-10
TRIGONOMETRY - TRIGONOMETRIC TABLE

USING TRIGONOMETRICAL TABLES –

Trigonometric Tables –

The tables of natural sines, cosines, tangents, etc., given with the continuation of this learning. The given values of these T-ratios upto 4 decimal place, and are known as Trigonometric tables.

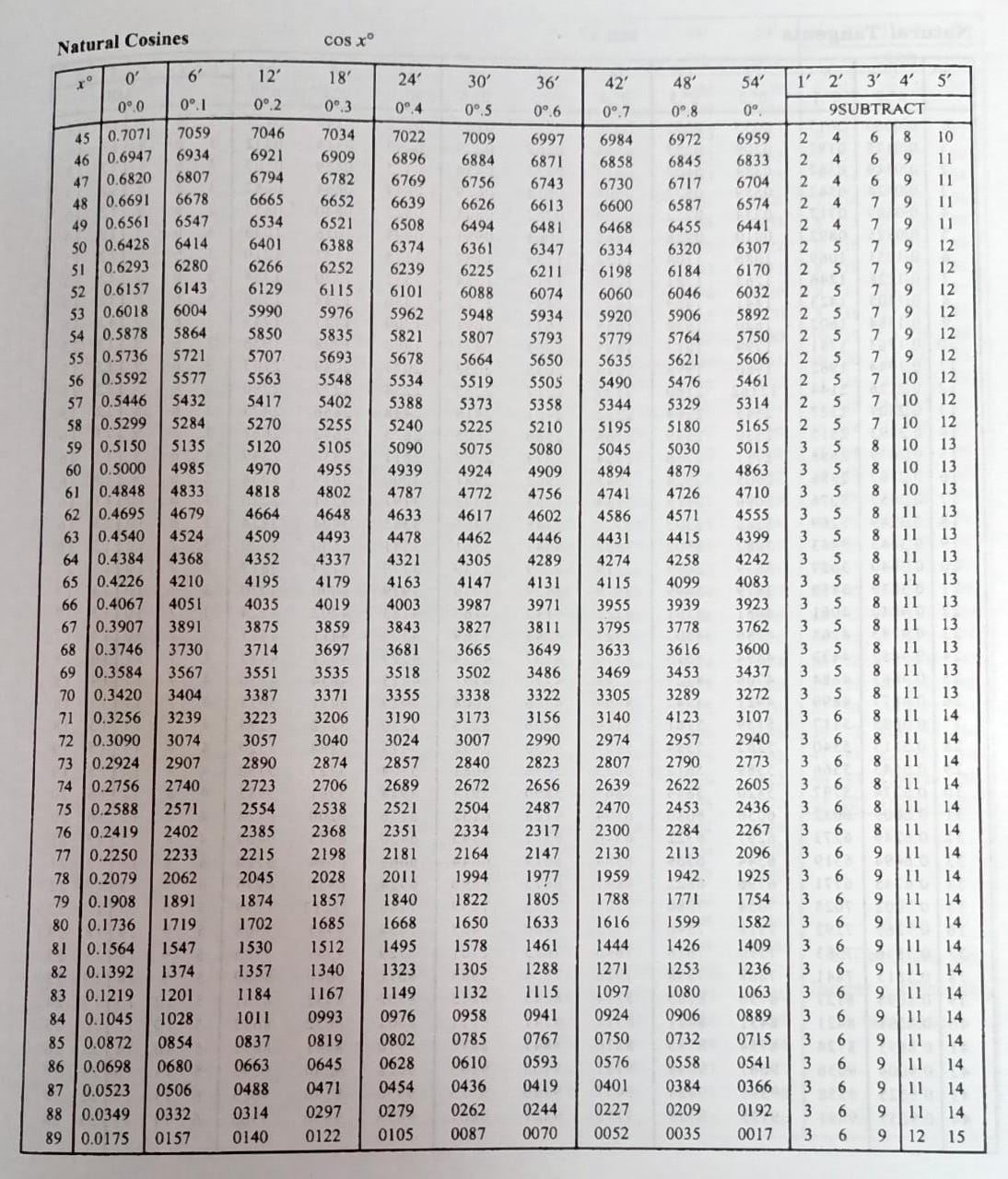
A Trigonometric table consists of three parts : -

(i) A column on the extreme left containing degrees from 0⁰ to 89⁰

(ii) Ten columns headed by 0ʹ, 6ʹ, 12ʹ, 18ʹ, 24ʹ, 30ʹ, 36ʹ, 42ʹ, 48ʹ, and 54ʹ

(iii) Five columns of mean difference, headed by 1ʹ, 2ʹ, 3ʹ, 4ʹ, and 5ʹ

An Important Note : -

(i) The mean difference is added in case of sines, tangents, and secants.

(ii) The mean difference is subtracted in case of cosines, cotangents, and cosecants.

The method of finding T-ratios of given angles using trigonometric tables, will be clear from the following examples,

Relation between Degree and Minutes –

         1⁰ =  60ʹ

           1

=>    (------)⁰  =  1ʹ

          60

                1

=>    6ʹ = (------ X 6)⁰

               60

                1

=>    6ʹ = (------)⁰ =  (0.10)⁰

               10

Thus,  (40.1)⁰ means 40⁰ 6ʹ

            (40.2)⁰ means 40⁰ 12ʹ and so on.

Example.1) Using tables, find the value of sin 43⁰ 52ʹ

Ans.)  We have, 43⁰ 52ʹ= 43⁰ 48ʹ + 4ʹ

In the table of natural sines, look at the number in the row against 43⁰ and in the column headed 48ʹ as shown below .

From the table of Natural Sines

Now, sin 43⁰ 48ʹ = 0.6921

Mean difference for 4ʹ = 0.0008  [to be added]

[see the number in the same row under 4ʹ]

sin 43⁰ 52ʹ = (0.6921 + 0.0008) =  0.6929     (Ans.)

Example.2) Using tables, find value of tan 38⁰ 27ʹ

Ans.)  We have, 38⁰ 27ʹ = 38⁰ 24ʹ + 3ʹ

In the table of natural tangents, look at the number in the row against 38⁰ and in the column headed 24ʹ, as shown below –

From Table of Natural Tangents

So, tan 38⁰ 24ʹ = 0.7926

Mean difference for 3ʹ = 0.0014 (to be added)    [see the number in the same row under 3ʹ]

  So, tan 38⁰ 27ʹ = (0.7926 + 0.0014) = 0.7940    (Ans.)

Example.3)  Using the tables, find the value of cos 24⁰ 17ʹ

Ans.)  We have, 24⁰ 17ʹ = 24⁰ 12ʹ + 5ʹ

In the table of natural cosines, look at the number in the row against 24⁰ and in the column headed by 12ʹ, as shown below –

From the table of Natural Cosines

So, cos 24⁰ 12ʹ = 0.9121

Mean difference for 5ʹ = 0.0006  (to be subtracted)  [see the number in the row under 5ʹ]

So, cos 24⁰ 17ʹ = (0.9121 – 0.0006) = 0.9115           (Ans.)

Larger is the angle, smaller is its cosines.

Your second block of text...